重置
序号 ID 年级 类型 来源 摘要 创建时间
18805 5c85c41f210b284290fc2a02 高中 解答题 自招竞赛 设 $J$ 为三角形 $ABC$ 顶点 $A$ 所对旁切圆的圆心。该旁切圆与边 $BC$ 相切于点 $M$，与直线 $AB$ 和 $AC$ 分别相切于点 $K$ 和 $L$．直线 $LM$ 和 $BJ$ 相交于点 $F$，直线 $KM$ 与 $CJ$ 相交于点 $G$．设 $S $ 是直线 $AF$ 和 $BC $ 的交点，$T$ 是直线 $AG $ 和 $BC$ 的交点．
证明：$M$ 是线段 $ST$ 的中点．（三角形 $ABC$ 的顶点 $A$ 所对的旁切圆是指与边 $BC$ 相切，并且与边 $AB$，$AC $ 的延长线相切的圆．）（希腊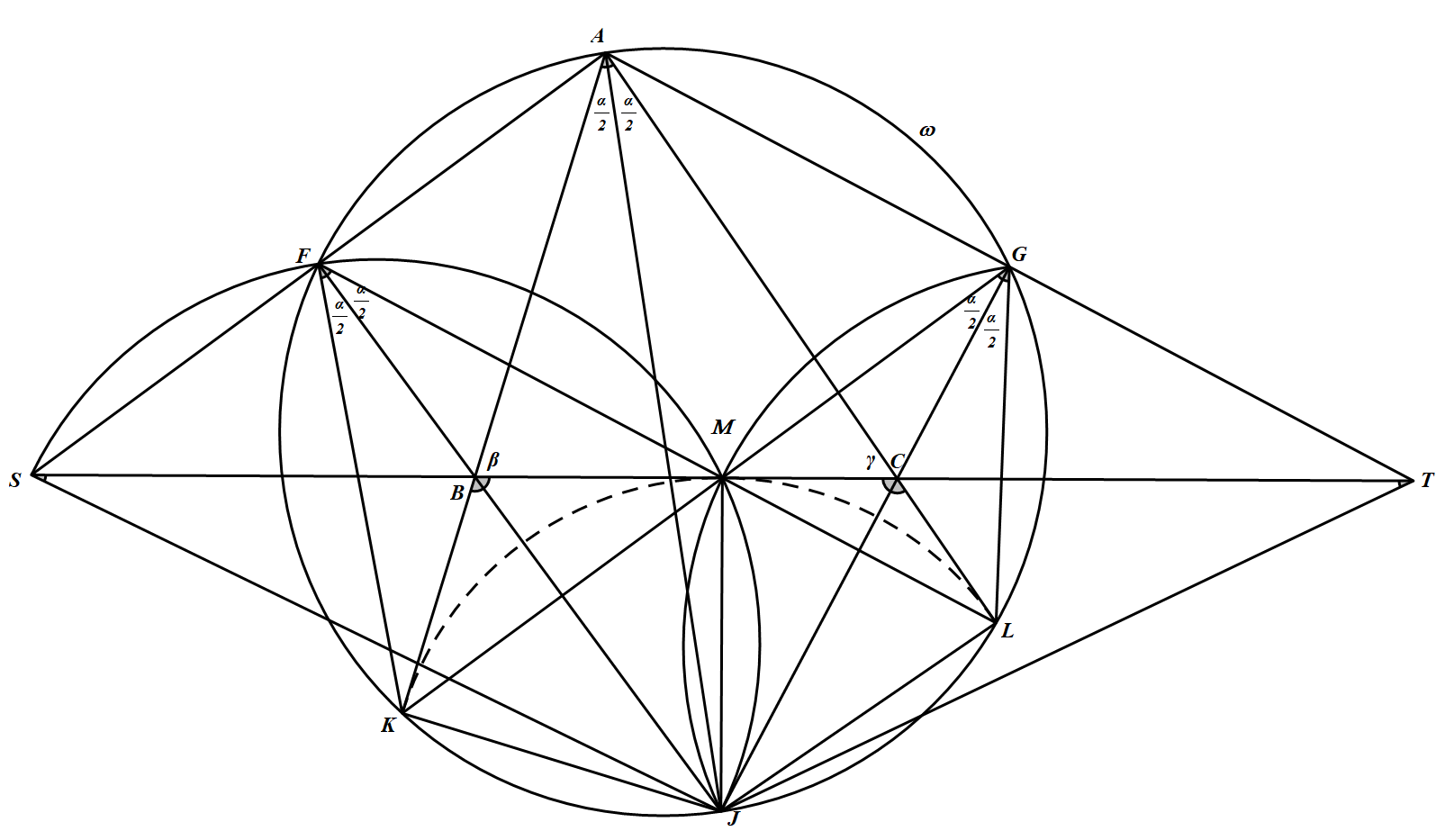）		 2022-04-17 19:46:44
18800 5c85c45b210b28428f14d396 高中 解答题 自招竞赛 已知三角形 $ABC $ 中，$\angle BCA=90{}^\circ $，$D$ 是过顶点 $C$ 的高的垂足．设 $X$ 是线段 $CD$ 内部的一点．$K$ 是线段 $AX$ 上一点，使得 $BK=BC$．$L$ 是线段 $BX$ 上一点，使得 $AL=AC$．设 $M$ 是 $AL$ 与 $BK $ 的交点。证明：$MK = ML$．（捷克） 2022-04-17 19:44:44
18773 5c85c8fc210b28428f14d3b9 高中 解答题 自招竞赛 设锐角三角形 $ABC$ 的外接圆为 $\Gamma$，$l$ 是圆 $\Gamma$ 的一条切线．记切线 $l$ 关于直线 $BC,CA$ 和 $AB$ 的对称直线分别为 $l_{a},l_{b}$ 和 $l_{c}$．证明：由直线 $l_{a},l_{b}$ 和 $l_{c}$ 构成的三角形的外接圆与圆 $\Gamma$ 相切．（日本） 2022-04-17 19:28:44
18769 5c85cdb2210b28428f14d3cb 高中 解答题 自招竞赛 设三角形 $ABC$ 的内心是 $I$，外接圆为 $\Gamma$．直线 $AI$ 交圆 $\Gamma$ 于另一点 $D$．设 $E$ 是弧 $\overparen{BDC}$ 上的一点，$F$ 是边 $BC$ 上的一点，使得 $\angle BAF=\angle CAE<\dfrac{1}{2}\angle BAC$．
设 $G$ 是线段 $IF$ 的中点．证明：直线 $DG$ 与 $EI$ 的交点在圆 $\Gamma$ 上．（中国香港）		 2022-04-17 19:27:44
18767 5c85cdc0210b28428f14d3d5 高中 解答题 自招竞赛 设 $P$ 是三角形 $ABC$ 内部的一点，直线 $AP,BP,CP$ 与三角形 $ABC$ 的外接圆 $\Gamma$ 的另一个交点分别为 $K,L,M$．圆 $\Gamma$ 在点 $C$ 处的切线与直线 $AB$ 相交于点 $S$．假设 $SC=SP$，证明：$MK=ML$．（波兰） 2022-04-17 19:27:44
18747 5c85d332210b284290fc2a4f 高中 解答题 自招竞赛 设 $O$ 是三角形 $ABC$ 的外心．点 $P$ 和 $Q$ 分别是边 $CA$ 和 $AB$ 的内点．设 $K,L$ 和 $M$ 分别是线段 $BP,CQ$ 和 $PQ$ 的中点，$\Gamma$ 是过点 $K,L$ 和 $M$ 的圆．若直线 $PQ$ 与圆 $\Gamma$ 相切，证明：$OP=OQ$．（俄罗斯） 2022-04-17 19:17:44
18735 5c85d340210b284290fc2a5b 高中 解答题 自招竞赛 在三角形 $ABC$ 中，$AB=AC$，$\angle CAB$ 和 $\angle ABC$ 的内角平分线分别与边 $BC$ 和 $CA$ 相交于点 $D$ 和 $E$．设 $K$ 是三角形 $ADC$ 的内心．若 $\angle BEK=45^{\circ}$，求 $\angle CAB$ 所有可能的值．（比利时） 2022-04-17 19:09:44
18725 5c85d6d9210b28428f14d3ff 高中 解答题 自招竞赛 已知 $H$ 是锐角三角形 $ABC$ 的垂心，以边 $BC$ 的中点为圆心，过点 $H$ 的圆与直线 $BC$ 相交于两点 $A_{1},A_{2}$；以边 $CA$ 的中点为圆心，过点 $H$ 的圆与直线 $CA$ 相交于两点 $B_{1},B_{2}$；以边 $AB$ 的中点为圆心，过点 $H$ 的圆与直线 $AB$ 相交于两点 $C_{1},C_{2}$．证明：六点 $A_{1},A_{2},B_{1},B_{2},C_{1},C_{2}$ 共圆．（俄罗斯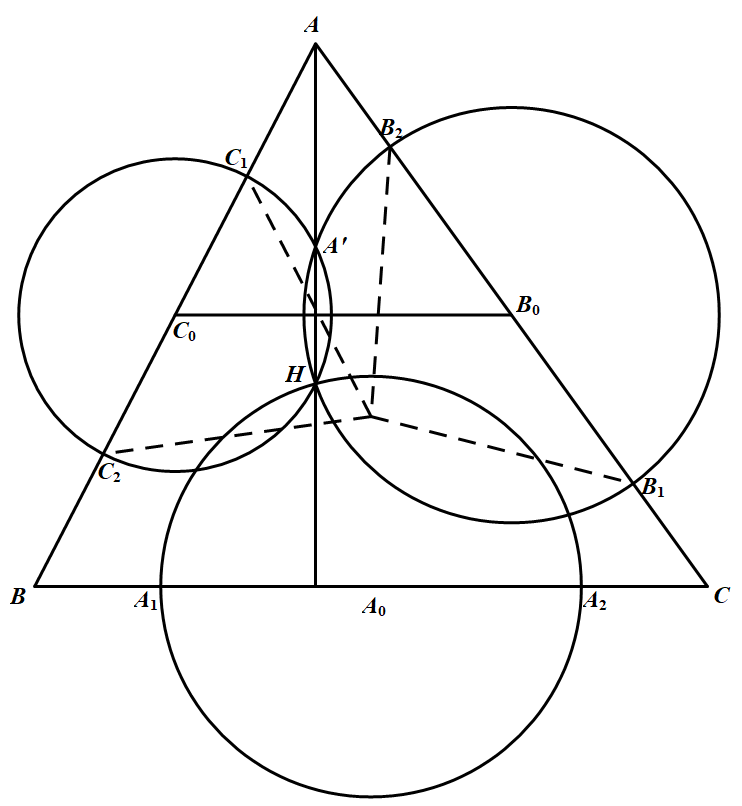） 2022-04-17 19:03:44
18719 5c85d6f7210b28428f14d415 高中 解答题 自招竞赛 在凸四边形 $ABCD$ 中，$BA\neq BC$．$\omega_{1}$ 和 $\omega_{2}$ 分别是 $\triangle ABC$ 和 $\triangle ADC$ 的内切圆．假设存在一个圆 $\omega$ 与射线 $BA$ 相切（切点不在线段 $BA$ 上），与射线 $BC$ 相切（切点不在线段BC上），且与直线 $AD$ 和直线 $CD$ 都相切．
证明：圆 $\omega_{1}$ 和 $\omega_{2}$ 的两条外公切线的交点在圆 $\omega$ 上．（俄罗斯）		 2022-04-17 19:00:44
18715 5c85dad8210b28428f14d42d 高中 解答题 自招竞赛 设 $A,B,C,D,E$ 五点中，$ABCD$ 是一个平行四边形，$BCED$ 是一个圆内接四边形．设 $\ell$ 是通过 $A$ 的一条直线，$\ell$ 与线段 $DC$ 交于点 $F$（$F$ 是线段 $DC$ 的内点），且 $\ell$ 与直线 $BC$ 交于点 $G$．若 $EF=EG=EC$，求证：$\ell$ 是 $\angle DAB$ 的角平分线．（卢森堡） 2022-04-17 19:57:43
18713 5c85dae4210b284290fc2a7a 高中 解答题 自招竞赛 在 $\triangle ABC$ 中，$\angle BCA$ 的角平分线与 $\triangle ABC$ 的外接圆交于点 $R$，与边 $BC$ 的垂直平分线交于点 $P$，与边 $AC$ 的垂直平分线交于点 $Q$．设 $K$ 与 $L$ 分别是边 $BC$ 和 $AC$ 的中点．证明：$\triangle RPK$ 和 $\triangle RQL$ 的面积相等．（捷克） 2022-04-17 19:57:43
18710 5c85de7c210b284290fc2a86 高中 解答题 自招竞赛 设 $I$ 为 $\triangle ABC$ 的内心，$P$ 是 $\triangle ABC$ 内部的一点，满足 $\angle PBA+\angle PCA=\angle PBC+\angle PCB$
证明：$AP\geqslant AI$，并说明等号成立的充分必要条件是 $P=I$．（韩国）		 2022-04-17 19:55:43
18705 5c85de9b210b28428f14d459 高中 解答题 自招竞赛 对于凸多边形 $P$ 的任意边 $b$，以 $b$ 为边，在 $P$ 内部作一个面积最大的三角形．证明：对 $P$ 的每条边，按上述方法所得三角形的面积之和至少是 $P$ 的面积的 $2$ 倍．（塞尔维亚） 2022-04-17 19:53:43
18704 5c85ed62210b284290fc2a99 高中 解答题 自招竞赛 在等边三角形 $ABC$ 的边上选取 $6$ 个点：在边 $BC$ 上选点 ${A}_{1}$ 和 ${A}_{2}$，在边 $CA$ 上选点 ${B}_{1}$ 和 ${B}_{2}$，在 边 $AB$ 上选点 ${C}_{1}$ 和 ${C}_{2}$，使得凸六边形 ${A}_{1}{A}_{2}{B}_{1}{B}_{2}{C}_{1}{C}_{2}$ 的边长都相等．证明：直线 ${A}_{1}{B}_{2},{B}_{1}{C}_{2},{C}_{1}{A}_{2}$ 共点．（罗马尼亚） 2022-04-17 19:52:43
18700 5c85ed8d210b28428f14d46f 高中 解答题 自招竞赛 给定凸四边形 $ABCD$，$BC=DA$，且 $BC$ 不平行 $AD$．设点 $E$ 和 $F$ 分别在边 $BC$ 和 $AD$ 的内部，满足 $BE=DF$．直线 $AC$ 和 $BD$ 相 交于点 $P$，直线 $BD$ 和 $EF$ 相 交于点 $Q$，直线 $EF$ 和 $AC$ 相交于点 $R$．证明：当点 $E$ 和 $F$ 变动时，三角形 $PQR$ 的外接圆经过除 点 $P$ 外的另一个定点．（波兰） 2022-04-17 19:49:43
18697 5c85f2b6210b28428f14d482 高中 解答题 自招竞赛 已知 三角形 $ABC$ 为锐角三角形，$AB≠AC$，以 $BC$ 直径为的圆分别交边 $AB$ 和 $AC$ 分别于 $M$ 和 $N$．记 $BC$ 的中点为边 $O$，$\angle BAC$ 的平分线和 $\angle MON$ 的平分线交于 $R$．求证：三角形 $BMR$ 的外接圆和三角形 $CNR$ 的外接圆有一个交点在边 $BC$ 上．（罗马尼亚） 2022-04-17 19:47:43
18632 5c85f2dc210b28428f14d48d 高中 解答题 自招竞赛 在凸四边形 $ABCD$ 中，对角线 $BD$ 既不是 $\angle ABC$ 的平分线，也不是 $\angle CDA$ 的平分线．点 $P$ 在四边形 $ABCD$ 内部，满足 $\angle PBC$ = $\angle DBA$ 和 $\angle PDC=\angle BDA$．证明：$ABCD$ 是圆内接四边形的充分必要条件是 $AP=CP$．（波兰） 2022-04-17 19:08:43
18549 5c85f64b210b284290fc2acf 高中 解答题 自招竞赛 给定一个凸六边形，其任意两条对边具有如下性质：它们的中点之间的距离等于它们长度之和的 $\dfrac{\sqrt{3}}{2}$ 倍．求证：该六边形的所有内角相等（一个凸六边形 $ABCDEF$ 有 $3$ 组对边：$AB$ 和 $DE$，$BC$ 和 $EF$，$CD$ 和 $FA$）．（波兰） 2022-04-17 19:25:42
18548 5c85f657210b28428f14d4a9 高中 解答题 自招竞赛 设 $ABCD$ 是一个圆内接四边形，点 $P,Q$ 和 $R$ 分别是 $D$ 到直线 $BC$、$CA$ 和 $AB$ 的射影．求证：$PQ=QR$ 的充要条件是 $\angle ABC$ 和 $\angle CDA$ 的角平分线的交点在 $AC$ 上．（芬兰） 2022-04-17 19:24:42
18541 5c85f8e1210b28428f14d4bf 高中 解答题 自招竞赛 $BC$ 为圆 $\Gamma$ 的直径，$\Gamma$ 的圆心为 $O$，$A$ 为 $\Gamma$ 上一点，$0^\circ<\angle AOB<120^\circ$，$D$ 是 $\overparen{AB}$（不含 $C$）的中点，过 $O$ 平行于 $DA$ 的直线交 $AC$ 于 $I$，$OA$ 的垂直平分线交 $\Gamma$ 于 $E,F$．求证：$I$ 是 $\triangle CEF$ 的内心．（韩国） 2022-04-17 19:21:42
0.181390s