查看数据源：5c85d6f7210b28428f14d415
在凸四边形 $ABCD$ 中，$BA\neq BC$．$\omega_{1}$ 和 $\omega_{2}$ 分别是 $\triangle ABC$ 和 $\triangle ADC$ 的内切圆．假设存在一个圆 $\omega$ 与射线 $BA$ 相切（切点不在线段 $BA$ 上），与射线 $BC$ 相切（切点不在线段BC上），且与直线 $AD$ 和直线 $CD$ 都相切．
证明：圆 $\omega_{1}$ 和 $\omega_{2}$ 的两条外公切线的交点在圆 $\omega$ 上．（俄罗斯）
【难度】
【出处】
2008年第49届IMO试题
【标注】
  • 知识点
    >
    二试几何部分
【答案】
略
【解析】
先证两个引理：
引理一：设 $ABCD$ 是凸四边形，圆 $\omega$ 与射线 $BA$（不包括线段 $BA$）相切，与射线 $BC$（不包括线段 $BC$）相切，且与直线 $AD$ 和直线 $CD$ 都相切．则 $AB+AD=CB+CD$．
引理一的证明：设直线 $AB,BC,CD,DA$ 分别与圆 $\omega$ 相切于点 $P,Q,R,S$，如图，则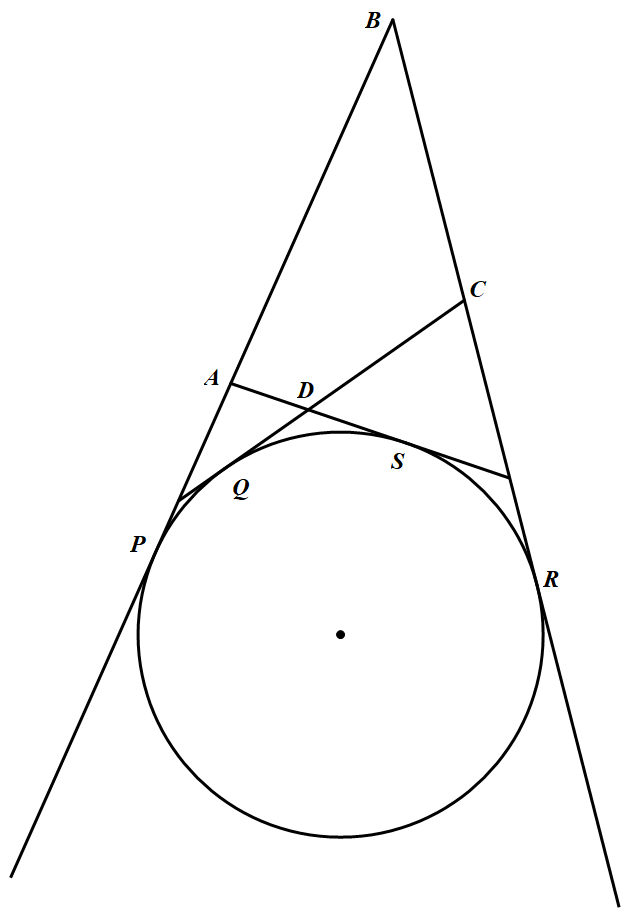$\begin{aligned}
&AB+AD=CB+CD\\
\Leftrightarrow& AB+(AD+DS)=CB+(CD+CR)\\
\Leftrightarrow& AB+AS=CB+CR\\
\Leftrightarrow& AB+AP=CB+CQ\\
\Leftrightarrow& BP=BR
\end{aligned}$
从而引理一得证．
引理二：设三个圆：$\odot O_1,\odot O_2,\odot O_3$ 的半径两两不等，则它们的外位似中心共线．
引理二的证明：设 $X_3$ 是 $\odot O_1$ 与 $\odot O_2$ 的外位似中心，$X_2$ 是 $\odot O_1$ 与 $\odot O_3$ 的外位似中心，$X_1$ 是 $\odot O_2$ 与 $\odot O_3$ 的外位似中心，$r_i$ 是 $\odot O_i(i=1,2,3)$ 的半径，由位似的性质知 $\dfrac{\overline{O_1X_3}}{X_3O_2}=-\dfrac{r_1}{r_2}$，这里的 $\overline{O_1X_3}$ 表示有向线段 $O_1X_3$，如图所示．同理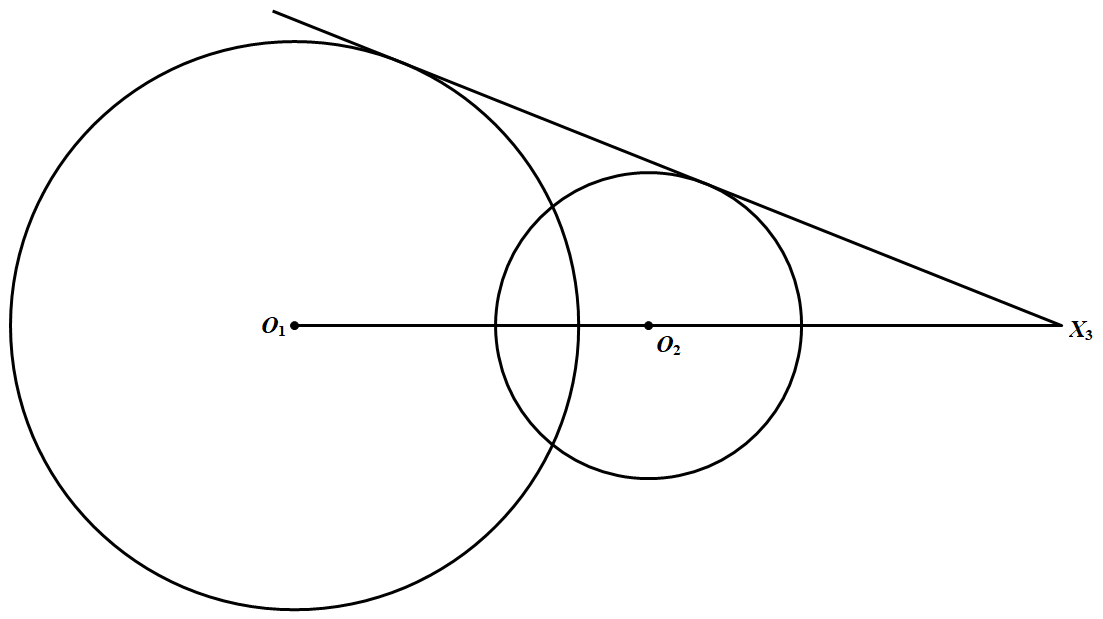$\dfrac{\overline{O_2X_1}}{X_1O_3}=-\dfrac{r_2}{r_3},\dfrac{\overline{O_3X_2}}{X_2O_1}=-\dfrac{r_3}{r_1}$
所以 $\dfrac{\overline{O_1X_3}}{X_3O_2}\cdot\dfrac{\overline{O_2X_1}}{X_1O_3}\cdot\dfrac{\overline{O_3X_2}}{X_2O_1}=\left(-\dfrac{r_1}{r_2}\right)\left(-\dfrac{r_2}{r_3}\right)\left(-\dfrac{r_3}{r_1}\right)=-1$
由梅内劳斯定理知，$X_1,X_2,X_3$ 三点共线．
设 $U,V$ 分别是 $\omega_1$ 和 $\omega_2$ 与 $AC$ 的切点，如图，则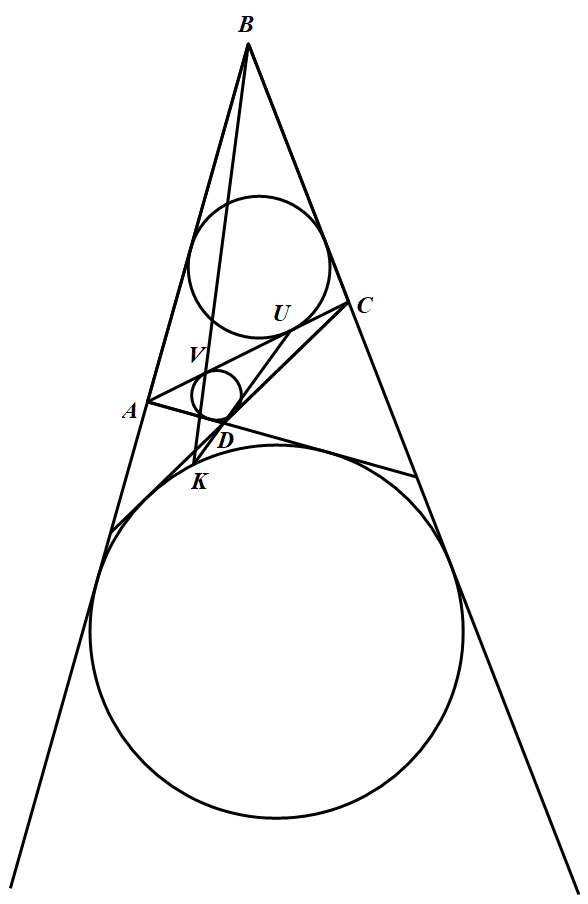$\begin{aligned}
AV&=\dfrac{AD+AC-CD}{2}=\dfrac{AC}{2}+\dfrac{AD-CD}{2}\\
&=\dfrac{AC}{2}+\dfrac{CB-AB}{2}=\dfrac{AC+CB-AB}{2}(由引理一)\\
&=CU
\end{aligned}$
所以，三角形 $ABC$ 的关于顶点 $B$ 的旁切圆 $\omega_3$ 与边 $AC$ 的切点亦为 $V$．因此，$\omega_2$ 与 $\omega_3$ 内切与点 $V$，即 $V$ 为 $\omega_2$ 与 $\omega_3$ 的外位似中心．设 $K$ 是 $\omega_1$ 与 $\omega_2$ 的外位似中心（即两条外公切线的交点），由引理二知，$K,V,B$ 三点共线．
完全类似地可得 $K,D,U$ 三点共线．
因为 $BA\ne BC$，所以 $U\ne V$（否则，由 $AV=CU$ 知，$U=V$ 是边 $AC$ 的中点，与 $BA\ne BC$ 矛盾．）所以，直线 $BV$ 与 $DU$ 不重合．故 $K=BV\bigcap DU$．
于是只需证明直线 $BV$ 与 $DU$ 的交点在圆 $\omega$ 上．
作圆 $\omega$ 的一条平行于 $AC$ 的切线 $l$（靠近边 $AC$ 的那条），设 $l$ 与圆 $\omega$ 相切于点 $T$，下证 $B,V,T$ 三点共线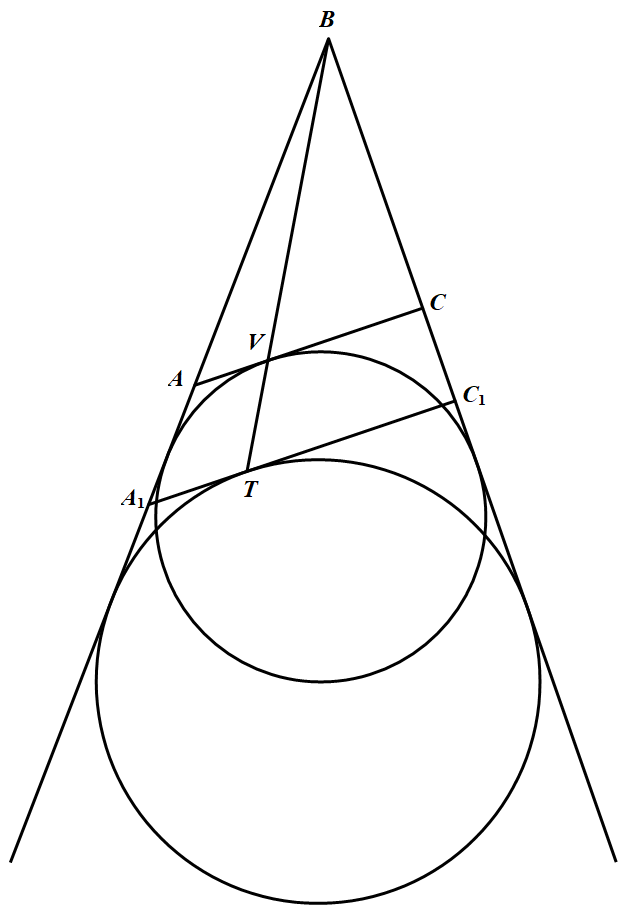．如上图，设 $l$ 与射线 $BA,BC$ 分别交于点 $A_1,C_1$，则圆 $\omega$ 是三角形 $BA_1C_1$ 的关于顶点 $B$ 的旁切圆，$T$ 是它与 $A_1C_1$ 的切点，而圆 $\omega_3$ 是三角形 $BAC$ 关于点 $B$ 的旁切圆，圆 $\omega_3$ 与 $AC$ 相切于点 $V$．则由 $A_1C_1\parallel AC$ 知，$\triangle BAC$ 与 $\triangle BA_1C_1$ 以 $B$ 为中心位似，而 $V,T$ 分别是对应旁切圆与对应边的切点，因此 $V,T$ 是这一对位似形中的对应点，而 $B$ 是位似中心，故 $B,V,T$ 共线．从而命题得证．
答案 解析 备注
0.133217s