设 $J$ 为三角形 $ABC$ 顶点 $A$ 所对旁切圆的圆心。该旁切圆与边 $BC$ 相切于点 $M$,与直线 $AB$ 和 $AC$ 分别相切于点 $K$ 和 $L$.直线 $LM$ 和 $BJ$ 相交于点 $F$,直线 $KM$ 与 $CJ$ 相交于点 $G$.设 $S $ 是直线 $AF$ 和 $BC $ 的交点,$T$ 是直线 $AG $ 和 $BC$ 的交点.
证明:$M$ 是线段 $ST$ 的中点.(三角形 $ABC$ 的顶点 $A$ 所对的旁切圆是指与边 $BC$ 相切,并且与边 $AB$,$AC $ 的延长线相切的圆.)(希腊)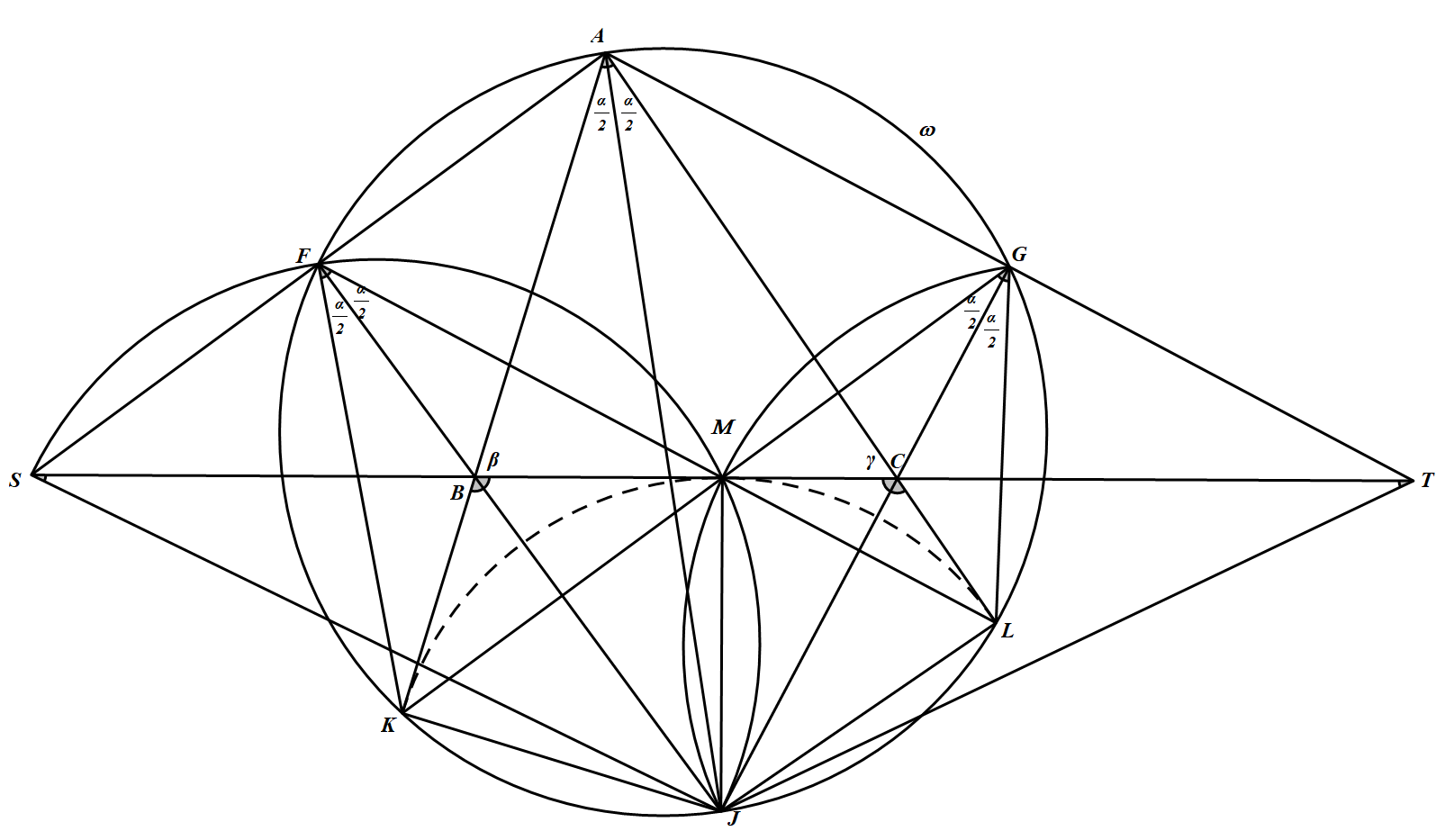
证明:$M$ 是线段 $ST$ 的中点.(三角形 $ABC$ 的顶点 $A$ 所对的旁切圆是指与边 $BC$ 相切,并且与边 $AB$,$AC $ 的延长线相切的圆.)(希腊)

【难度】
【出处】
2012年第53届IMO试题
【标注】
【答案】
略
【解析】
设 $\angle CAB=\alpha,\angle ABC=\beta,\angle BCA=\gamma$.由于 $AJ$ 是 $\angle CAB$ 的角平分线,所以 $\angle JAK=\angle JAL=\dfrac{\alpha}{2}$.因为 $\angle AKJ=\angle ALJ=90^\circ$,所以点 $K$ 和 $L$ 在以 $AJ$ 为直径的圆 $\omega$ 上.
因为 $BJ$ 是 $\angle KBM$ 的角平分线,所以 $\angle MBJ=90^\circ-\dfrac{\beta}{2}$,而 $\triangle KBM$ 是等腰三角形,所以 $\angle BMK=\dfrac{\beta}{2}$.同理,$\angle MCJ=90^\circ-\dfrac{\gamma}{2},\angle CML=\dfrac{\gamma}{2}$.于是
$\angle LFJ=\angle MBJ-\angle BMF=\angle MBJ-\angle CML=\left(90^\circ-\dfrac{\beta}{2}\right)-\dfrac{\gamma}{2}=\dfrac{\alpha}{2}=\angle LAJ$.
所以,点 $F$ 在圆 $\omega$ 上.同理,点 $G$ 也在圆 $\omega$ 上.由于 $AJ$ 为圆 $\omega$ 的直径,故
$\angle AFJ=\angle AGJ=90^\circ$.
直线 $AB$ 与 $BC$ 是关于 $\angle ABC$ 的外角平分线 $BF$ 对称的,又因为 $AF\perp BF,KM\perp BF$,所以,线段 $SM$ 与 $AK$ 是关于 $BF$ 对称的,故 $SM=AK$,同理 $TM=AL$.
而 $AK=AL$,所以 $SM=TM$.
因为 $BJ$ 是 $\angle KBM$ 的角平分线,所以 $\angle MBJ=90^\circ-\dfrac{\beta}{2}$,而 $\triangle KBM$ 是等腰三角形,所以 $\angle BMK=\dfrac{\beta}{2}$.同理,$\angle MCJ=90^\circ-\dfrac{\gamma}{2},\angle CML=\dfrac{\gamma}{2}$.于是
$\angle LFJ=\angle MBJ-\angle BMF=\angle MBJ-\angle CML=\left(90^\circ-\dfrac{\beta}{2}\right)-\dfrac{\gamma}{2}=\dfrac{\alpha}{2}=\angle LAJ$.
所以,点 $F$ 在圆 $\omega$ 上.同理,点 $G$ 也在圆 $\omega$ 上.由于 $AJ$ 为圆 $\omega$ 的直径,故
$\angle AFJ=\angle AGJ=90^\circ$.
直线 $AB$ 与 $BC$ 是关于 $\angle ABC$ 的外角平分线 $BF$ 对称的,又因为 $AF\perp BF,KM\perp BF$,所以,线段 $SM$ 与 $AK$ 是关于 $BF$ 对称的,故 $SM=AK$,同理 $TM=AL$.
而 $AK=AL$,所以 $SM=TM$.
答案
解析
备注