已知 $H$ 是锐角三角形 $ABC$ 的垂心,以边 $BC$ 的中点为圆心,过点 $H$ 的圆与直线 $BC$ 相交于两点 $A_{1},A_{2}$;以边 $CA$ 的中点为圆心,过点 $H$ 的圆与直线 $CA$ 相交于两点 $B_{1},B_{2}$;以边 $AB$ 的中点为圆心,过点 $H$ 的圆与直线 $AB$ 相交于两点 $C_{1},C_{2}$.证明:六点 $A_{1},A_{2},B_{1},B_{2},C_{1},C_{2}$ 共圆.(俄罗斯)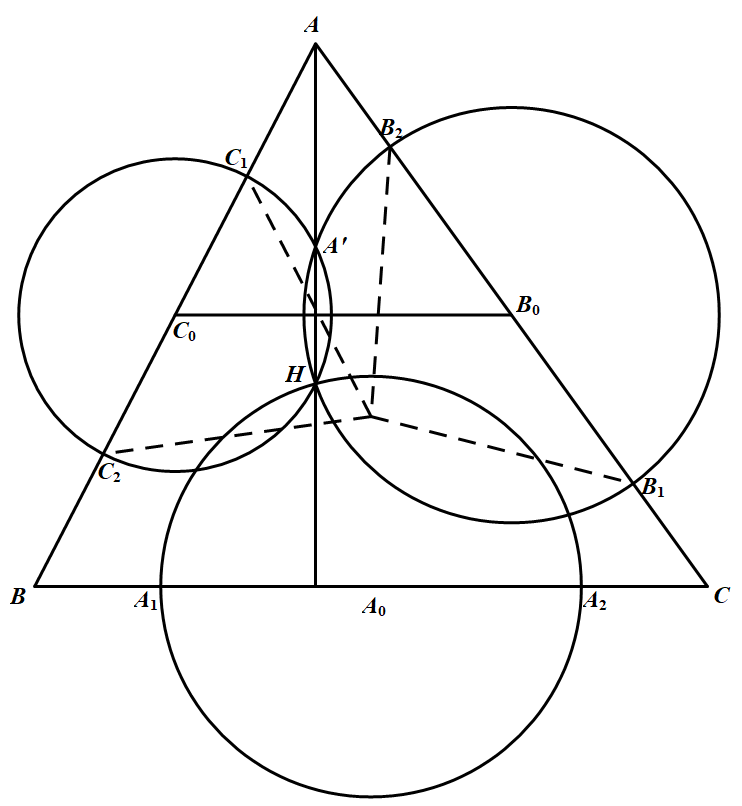

【难度】
【出处】
2008年第49届IMO试题
【标注】
【答案】
略
【解析】
证法一
$B_0,C_0$ 分别是边 $CA,AB$ 的中点.设以边 $B_0$ 为圆心,过点 $H$ 的圆与以 $C_0$ 为圆心,过点 $H$ 的圆的另一个交点为 $A^\prime$,则 $A^\prime H\perp C_0B_0$.由于 $B_0,C_0$ 分别是边 $CA,AB$ 的中点,所以 $C_0B_0\parallel BC$,从而 $A^\prime H\perp BC$,于是点 $A^\prime$ 在 $AH$ 上.
由切割线定理:
$AC_1\cdot AC_2=AA^\prime \cdot AH=AB_1\cdot AB_2$
所以,$B_1,B_2,C_1,C_2$ 四点共圆.
分别作 $B_1B_2,C_1C_2$ 的垂直平分线,设它们相交于点 $O$,则 $O$ 是四边形 $B_1B_2C_1C_2$ 的外接圆圆心,也是 $\triangle ABC$ 的外心,且 $OB_1=OB_2=OC_1=OC_2$.
同理可得,$OA_1=OA_2=OB_1=OB_2$,所以,$A_1,A_2,B_1,B_2,C_1,C_2$ 六点都是在以 $O$ 为圆心,$OA_1$ 为半径的圆上,故六点 $A_1,A_2,B_1,B_2,C_1,C_2$ 共圆.
证明二
设三角形 $ABC$ 的外心为 $O,D,E,F$ 分别是边 $BC,CA,AB$ 上的中点,连接 $DF$,交 $BH$ 于点 $P$,则 $BH\perp DF$,于是由勾股定理得
$BF^2-FH^2=BP^2-PH^2=BD^2-DH^2$ ①
$BO^2-A_1O^2=BD^2-A_1D^2=BD^2-DH^2$ ②
同理可得 $BO^2-C_2O^2=BF^2-FH^2$ ③
所以,由 ①,②,③ 可得,$A_1O=C_2O$.
易知 $A_1O=A_2O,C_1O=C_2O$,故 $A_1O=A_2O=C_1O=C_2O$.
同理,$A_1O=A_2O=B_1O=B_2O$,所以,六点 $A_1,A_2,B_1,B_2,C_1,C_2$ 在以 $O$ 为圆心的圆上.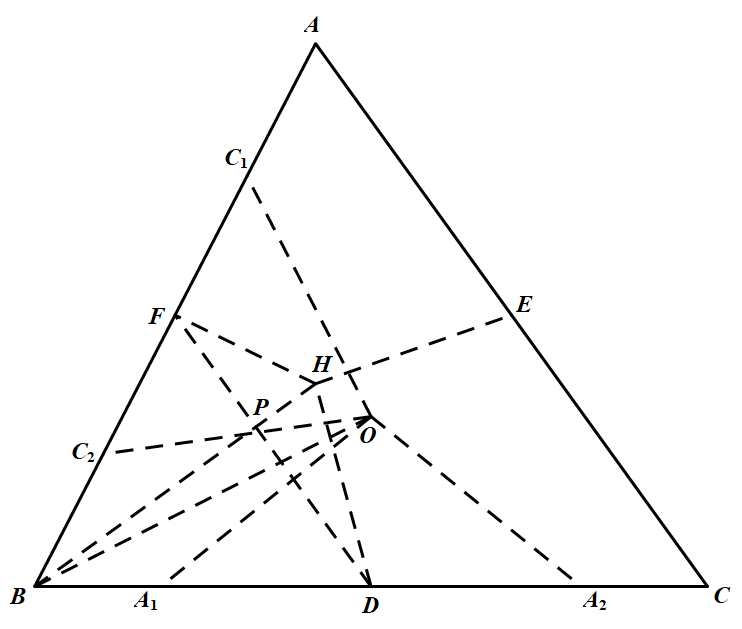
$B_0,C_0$ 分别是边 $CA,AB$ 的中点.设以边 $B_0$ 为圆心,过点 $H$ 的圆与以 $C_0$ 为圆心,过点 $H$ 的圆的另一个交点为 $A^\prime$,则 $A^\prime H\perp C_0B_0$.由于 $B_0,C_0$ 分别是边 $CA,AB$ 的中点,所以 $C_0B_0\parallel BC$,从而 $A^\prime H\perp BC$,于是点 $A^\prime$ 在 $AH$ 上.
由切割线定理:
$AC_1\cdot AC_2=AA^\prime \cdot AH=AB_1\cdot AB_2$
所以,$B_1,B_2,C_1,C_2$ 四点共圆.
分别作 $B_1B_2,C_1C_2$ 的垂直平分线,设它们相交于点 $O$,则 $O$ 是四边形 $B_1B_2C_1C_2$ 的外接圆圆心,也是 $\triangle ABC$ 的外心,且 $OB_1=OB_2=OC_1=OC_2$.
同理可得,$OA_1=OA_2=OB_1=OB_2$,所以,$A_1,A_2,B_1,B_2,C_1,C_2$ 六点都是在以 $O$ 为圆心,$OA_1$ 为半径的圆上,故六点 $A_1,A_2,B_1,B_2,C_1,C_2$ 共圆.
证明二
设三角形 $ABC$ 的外心为 $O,D,E,F$ 分别是边 $BC,CA,AB$ 上的中点,连接 $DF$,交 $BH$ 于点 $P$,则 $BH\perp DF$,于是由勾股定理得
$BF^2-FH^2=BP^2-PH^2=BD^2-DH^2$ ①
$BO^2-A_1O^2=BD^2-A_1D^2=BD^2-DH^2$ ②
同理可得 $BO^2-C_2O^2=BF^2-FH^2$ ③
所以,由 ①,②,③ 可得,$A_1O=C_2O$.
易知 $A_1O=A_2O,C_1O=C_2O$,故 $A_1O=A_2O=C_1O=C_2O$.
同理,$A_1O=A_2O=B_1O=B_2O$,所以,六点 $A_1,A_2,B_1,B_2,C_1,C_2$ 在以 $O$ 为圆心的圆上.

答案
解析
备注