在 $\triangle ABC$ 中，$\angle BCA$ 的角平分线与 $\triangle ABC$ 的外接圆交于点 $R$，与边 $BC$ 的垂直平分线交于点 $P$，与边 $AC$ 的垂直平分线交于点 $Q$．设 $K$ 与 $L$ 分别是边 $BC$ 和 $AC$ 的中点．证明：$\triangle RPK$ 和 $\triangle RQL$ 的面积相等．（捷克）
【难度】
【出处】
2007年第48届IMO试题
【标注】
【答案】
略
【解析】
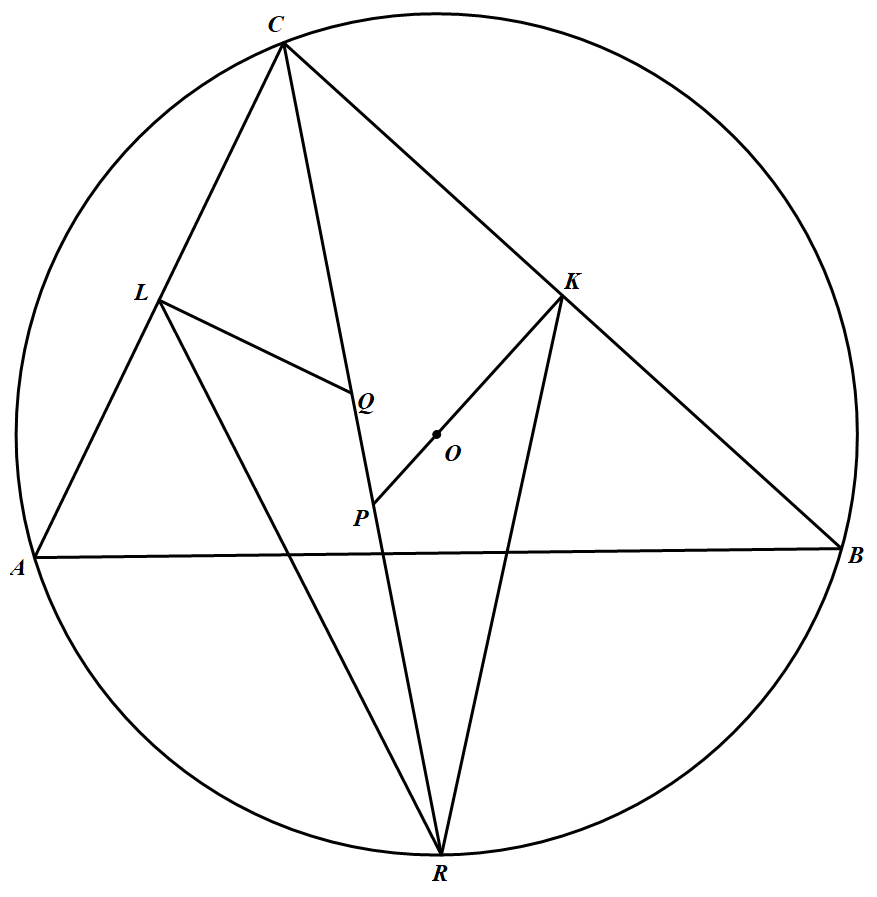如果 $AC=BC$，则 $\triangle ABC$ 是等腰三角形，$\triangle RQL$ 和 $\triangle RPK$ 关于角平分线 $CR$ 是对称的，结论明显成立．如果 $AC\ne BC$，不妨设 $AC<BC$．用 $O$ 表示 $\triangle ABC$ 的外心，注意到直角 $\triangle CLQ$ 与直角 $\triangle CKP$ 是相似的，所以
$\angle CPK=\angle CQL=\angle OQP$，且 $\dfrac{QL}{PK}=\dfrac{CQ}{CP}$ ①
设 $l$ 是弦 $CR$ 的垂直平分线，则 $l$ 过外心 $O$．
由于 $\triangle OPQ$ 是的等腰三角形，所以点 $P$ 和 $Q$ 是 $CR$ 上关于 $l$ 对称的两点，所以
$RP=CQ$ 且 $RQ=CP$ ②
因此由 ①② 有
$\begin{aligned}
\frac{S(\triangle RQL)}{S(\triangle RPK)}&=\frac{\frac{1}{2}RQ\cdot QL\cdot \sin\angle RQL}{\frac{1}{2}RP\cdot PK\cdot \sin\angle RPK}\\
&=\frac{RQ}{RP}\cdot\frac{QL}{PK}\\
&=\frac{CP}{CQ}\cdot\frac{CQ}{CP}\\
&=1
\end{aligned}$
因此 $S(\triangle RQL)=S(\triangle RPK)$．
答案
解析
备注
