在等边三角形 $ABC$ 的边上选取 $6$ 个点:在边 $BC$ 上选点 ${A}_{1}$ 和 ${A}_{2}$,在边 $CA$ 上选点 ${B}_{1}$ 和 ${B}_{2}$,在 边 $AB$ 上选点 ${C}_{1}$ 和 ${C}_{2}$,使得凸六边形 ${A}_{1}{A}_{2}{B}_{1}{B}_{2}{C}_{1}{C}_{2}$ 的边长都相等.证明:直线 ${A}_{1}{B}_{2},{B}_{1}{C}_{2},{C}_{1}{A}_{2}$ 共点.(罗马尼亚)
【难度】
【出处】
2005年第46届IMO试题
【标注】
【答案】
略
【解析】
记 $A_1A_2=d,AB=a$,另作一个边长为 $a-d$ 的正三角形 $A_0B_0C_0$,分别在边 $B_0C_0,C_0A_0,A_0B_0$ 上取点 $A^\prime,B^\prime,C^\prime$,使得 $A^\prime C_0=A_2 C,B^\prime A_0=B_2A,C^\prime B_0=C_2B$,则
$A^\prime B_0=a-d-A^\prime C_0=BC-A_1A_2-A_2C=BA_1$
同理可得 $B^\prime C_0=B_1C,C^\prime A_0=C_1A$.
结合 $\angle B_1CA_2=\angle B^\prime C_0A^\prime,\angle B_2AC_1=\angle B^\prime A_0C^\prime,\angle C_2BA_1=\angle C^\prime B_0A^\prime$,知
$\triangle CB_1A_2\cong\triangle C_0B^\prime A^\prime,\triangle AC_1B_2\cong\triangle A_0C^\prime B^\prime,\triangle BA_1C_2\cong\triangle B_0A^\prime C^\prime$
所以 $B^\prime C^\prime=C^\prime A^\prime =A^\prime B^\prime =d$
故三角形 $A^\prime B^\prime C^\prime$ 是正三角形,所以
$\angle A^\prime C^\prime B^\prime=\angle C^\prime B^\prime A^\prime=\angle A^\prime B^\prime C^\prime=60^\circ$
$\angle AB_2C_1=\angle A_0B^\prime C^\prime=180^\circ-\angle C^\prime B^\prime A^\prime-\angle A^\prime B^\prime C_0=120^\circ-\angle A^\prime B^\prime C_0$
所以 $\angle C_1B_2B_1=\angle B_1A_2A_1$
结合 $B_2C_1=B_1B_2=A_2B_1=A_1A_2=d$,知 $\triangle C_1B_2B_1\cong\triangle B_1A_2A_1$
所以 $B_1C_1=A_1B_1$,又 $C_1C_2=A_1C_2$,于是 $C_2B_1$ 是 $A_1C_1$ 的垂直平分线,所以 $C_2B_1$ 是 $\triangle A_1B_1C_1$ 的边 $A_1C_1$ 上的高,同理,$C_1A_2,A_1B_2$ 分别是 $\triangle A_1B_1C_1$ 的边 $A_1B_1,B_1C_1$ 上的高,故 $A_1B_2,B_1C_2,C_1A_2$ 共点.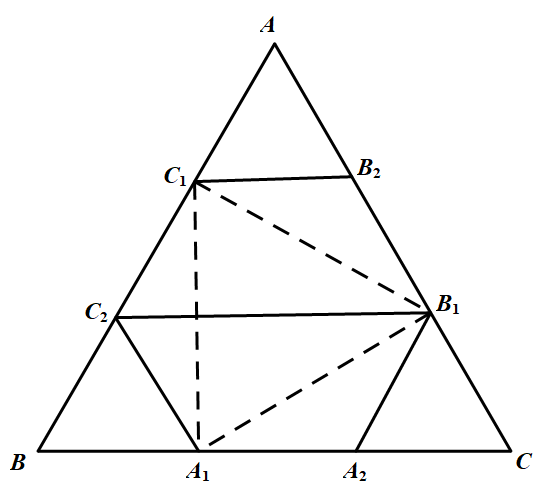
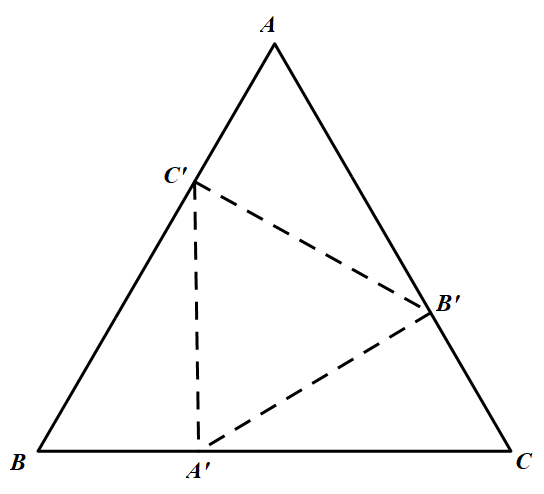
$A^\prime B_0=a-d-A^\prime C_0=BC-A_1A_2-A_2C=BA_1$
同理可得 $B^\prime C_0=B_1C,C^\prime A_0=C_1A$.
结合 $\angle B_1CA_2=\angle B^\prime C_0A^\prime,\angle B_2AC_1=\angle B^\prime A_0C^\prime,\angle C_2BA_1=\angle C^\prime B_0A^\prime$,知
$\triangle CB_1A_2\cong\triangle C_0B^\prime A^\prime,\triangle AC_1B_2\cong\triangle A_0C^\prime B^\prime,\triangle BA_1C_2\cong\triangle B_0A^\prime C^\prime$
所以 $B^\prime C^\prime=C^\prime A^\prime =A^\prime B^\prime =d$
故三角形 $A^\prime B^\prime C^\prime$ 是正三角形,所以
$\angle A^\prime C^\prime B^\prime=\angle C^\prime B^\prime A^\prime=\angle A^\prime B^\prime C^\prime=60^\circ$
$\angle AB_2C_1=\angle A_0B^\prime C^\prime=180^\circ-\angle C^\prime B^\prime A^\prime-\angle A^\prime B^\prime C_0=120^\circ-\angle A^\prime B^\prime C_0$
所以 $\angle C_1B_2B_1=\angle B_1A_2A_1$
结合 $B_2C_1=B_1B_2=A_2B_1=A_1A_2=d$,知 $\triangle C_1B_2B_1\cong\triangle B_1A_2A_1$
所以 $B_1C_1=A_1B_1$,又 $C_1C_2=A_1C_2$,于是 $C_2B_1$ 是 $A_1C_1$ 的垂直平分线,所以 $C_2B_1$ 是 $\triangle A_1B_1C_1$ 的边 $A_1C_1$ 上的高,同理,$C_1A_2,A_1B_2$ 分别是 $\triangle A_1B_1C_1$ 的边 $A_1B_1,B_1C_1$ 上的高,故 $A_1B_2,B_1C_2,C_1A_2$ 共点.


答案
解析
备注