设 $P$ 是三角形 $ABC$ 内部的一点，直线 $AP,BP,CP$ 与三角形 $ABC$ 的外接圆 $\Gamma$ 的另一个交点分别为 $K,L,M$．圆 $\Gamma$ 在点 $C$ 处的切线与直线 $AB$ 相交于点 $S$．假设 $SC=SP$，证明：$MK=ML$．（波兰）
【难度】
【出处】
2010年第51届IMO试题
【标注】
【答案】
略
【解析】
不妨设 $CA>CB$，则点 $S$ 在射线 $AB$ 上．
设直线 $SP$ 与三角形 $ABC$ 的外接圆相交于点 $E,F$，如图．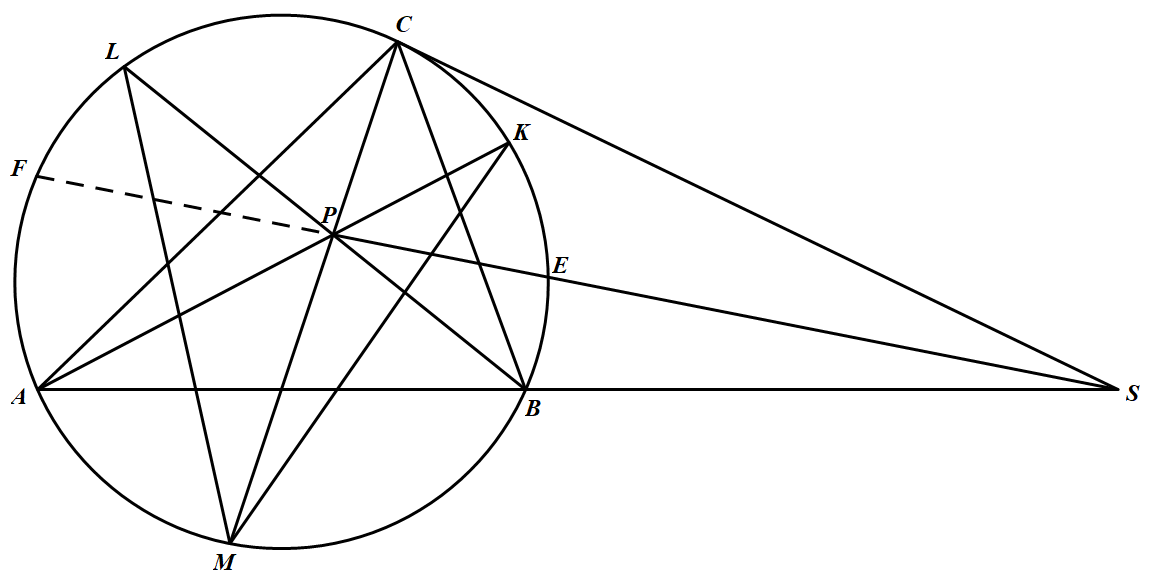
由题设及圆幂定理知 $SP^2=SC^2=SB\cdot SA$
所以 $\dfrac{SP}{SB}=\dfrac{SA}{SP}$，故 $\triangle PSA\sim \triangle BSP$，所以 $\angle BPS=\angle SAP$．
因为 $2\angle BPS =\overparen{BE}+\overparen{LF},2\angle SAP=\overparen{BE}+\overparen{EK}$，所以
$\overparen{LF}=\overparen{EK}$ ①
又由 $\angle SPC=\angle SCP$，可得，$\overparen{EC}+\overparen{MF}=\overparen{EC}+\overparen{EM}$，所以
$\overparen{MF}=\overparen{EM}$ ②
由 ①，② 可得
$\overparen{MFL}=\overparen{MF}+\overparen{FL}=\overparen{ME}+\overparen{EK}=\overparen{MEK}$
所以，$\overparen{MK}=\overparen{ML}$．
设直线 $SP$ 与三角形 $ABC$ 的外接圆相交于点 $E,F$，如图．
由题设及圆幂定理知 $SP^2=SC^2=SB\cdot SA$所以 $\dfrac{SP}{SB}=\dfrac{SA}{SP}$，故 $\triangle PSA\sim \triangle BSP$，所以 $\angle BPS=\angle SAP$．
因为 $2\angle BPS =\overparen{BE}+\overparen{LF},2\angle SAP=\overparen{BE}+\overparen{EK}$，所以
$\overparen{LF}=\overparen{EK}$ ①
又由 $\angle SPC=\angle SCP$，可得，$\overparen{EC}+\overparen{MF}=\overparen{EC}+\overparen{EM}$，所以
$\overparen{MF}=\overparen{EM}$ ②
由 ①，② 可得
$\overparen{MFL}=\overparen{MF}+\overparen{FL}=\overparen{ME}+\overparen{EK}=\overparen{MEK}$
所以，$\overparen{MK}=\overparen{ML}$．
答案
解析
备注
