$BC$ 为圆 $\Gamma$ 的直径，$\Gamma$ 的圆心为 $O$，$A$ 为 $\Gamma$ 上一点，$0^\circ<\angle AOB<120^\circ$，$D$ 是 $\overparen{AB}$（不含 $C$）的中点，过 $O$ 平行于 $DA$ 的直线交 $AC$ 于 $I$，$OA$ 的垂直平分线交 $\Gamma$ 于 $E,F$．求证：$I$ 是 $\triangle CEF$ 的内心．（韩国）
【难度】
【出处】
2002年第43届IMO试题
【标注】
【答案】
略
【解析】
显然 $CA$ 平分 $\angle ECF$．
如图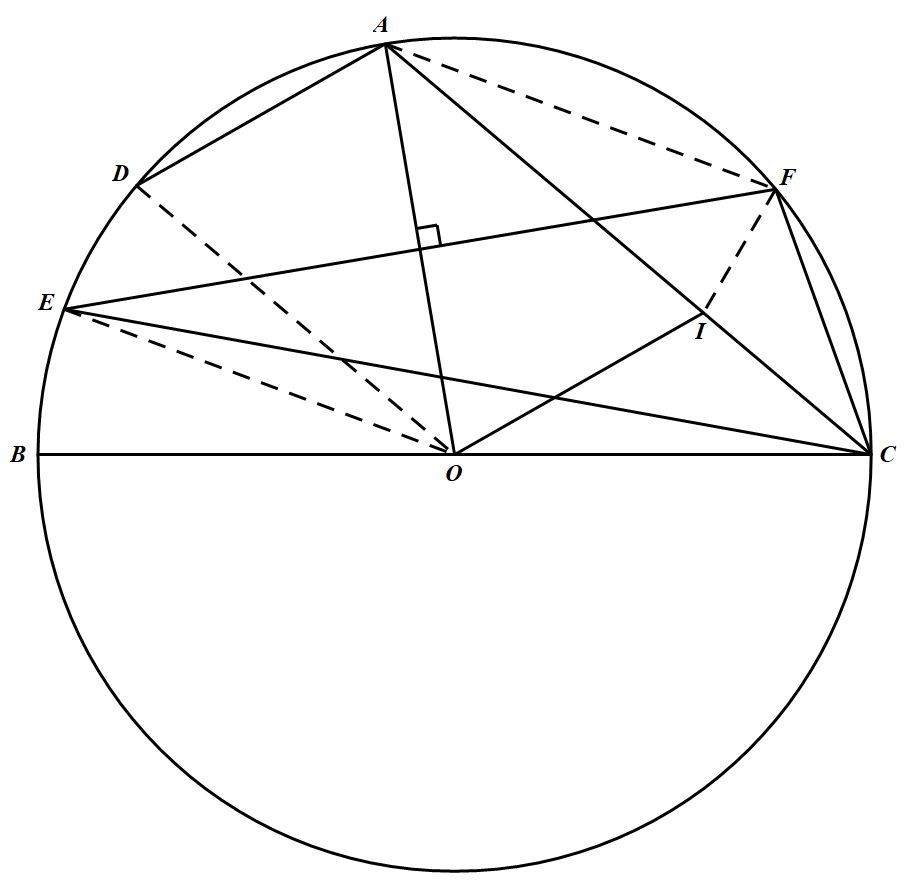
联结 $DO$，易见
$\angle DOA=\dfrac{1}{2}\angle AOB=\angle OAC$
故 $DO\parallel AC$，又 $DA\parallel OI$，故四边形 $ADOI$ 是平行四边形，故 $AI=OD=OE$，
又四边形 $AEOF$ 为菱形，因此，$OE=AF$，于是
$AI=AF$
故
$\begin{aligned}
\angle IFE&=\angle IFA-\angle EFA\\
&=\angle AIF-\angle ECA\\
&=\angle AIF-\angle ICF\\
&=\angle IFC
\end{aligned}$
即 $IF$ 平分 $\angle EFC$，故 $I$ 为 $\triangle CEF$ 内心．
如图
联结 $DO$，易见$\angle DOA=\dfrac{1}{2}\angle AOB=\angle OAC$
故 $DO\parallel AC$，又 $DA\parallel OI$，故四边形 $ADOI$ 是平行四边形，故 $AI=OD=OE$，
又四边形 $AEOF$ 为菱形，因此，$OE=AF$，于是
$AI=AF$
故
$\begin{aligned}
\angle IFE&=\angle IFA-\angle EFA\\
&=\angle AIF-\angle ECA\\
&=\angle AIF-\angle ICF\\
&=\angle IFC
\end{aligned}$
即 $IF$ 平分 $\angle EFC$，故 $I$ 为 $\triangle CEF$ 内心．
答案
解析
备注
