已知三角形 $ABC $ 中，$\angle BCA=90{}^\circ $，$D$ 是过顶点 $C$ 的高的垂足．设 $X$ 是线段 $CD$ 内部的一点．$K$ 是线段 $AX$ 上一点，使得 $BK=BC$．$L$ 是线段 $BX$ 上一点，使得 $AL=AC$．设 $M$ 是 $AL$ 与 $BK $ 的交点。证明：$MK = ML$．（捷克）
【难度】
【出处】
2012年第53届IMO试题
【标注】
【答案】
略
【解析】
设 $C^\prime$ 是 $C$ 关于直线 $AB$ 的对称点，$\omega_1$ 和 $\omega_2$ 分别是以 $A$ 和 $B$ 为圆心，$AL$ 和 $BK$ 为半径的圆．因为 $AC^\prime=AC=AL,BC^\prime=BC=BK$，所以，点 $C$ 和 $C^\prime$ 都在圆 $\omega_1$ 及 $\omega_2$ 上．由于 $\angle BCA=90^\circ$，所以，直线 $AC$ 与圆 $\omega_2$ 相切于点 $C$，直线 $BC$ 与圆 $\omega_1$ 相切于点 $C$．设 $K_1$ 是直线 $AX$ 与圆 $\omega_2$ 的不同于 $K$ 的另一个交点，$L_1$ 是直线 $BX$ 与圆 $\omega_1$ 的不同于 $L$ 的另一个交点．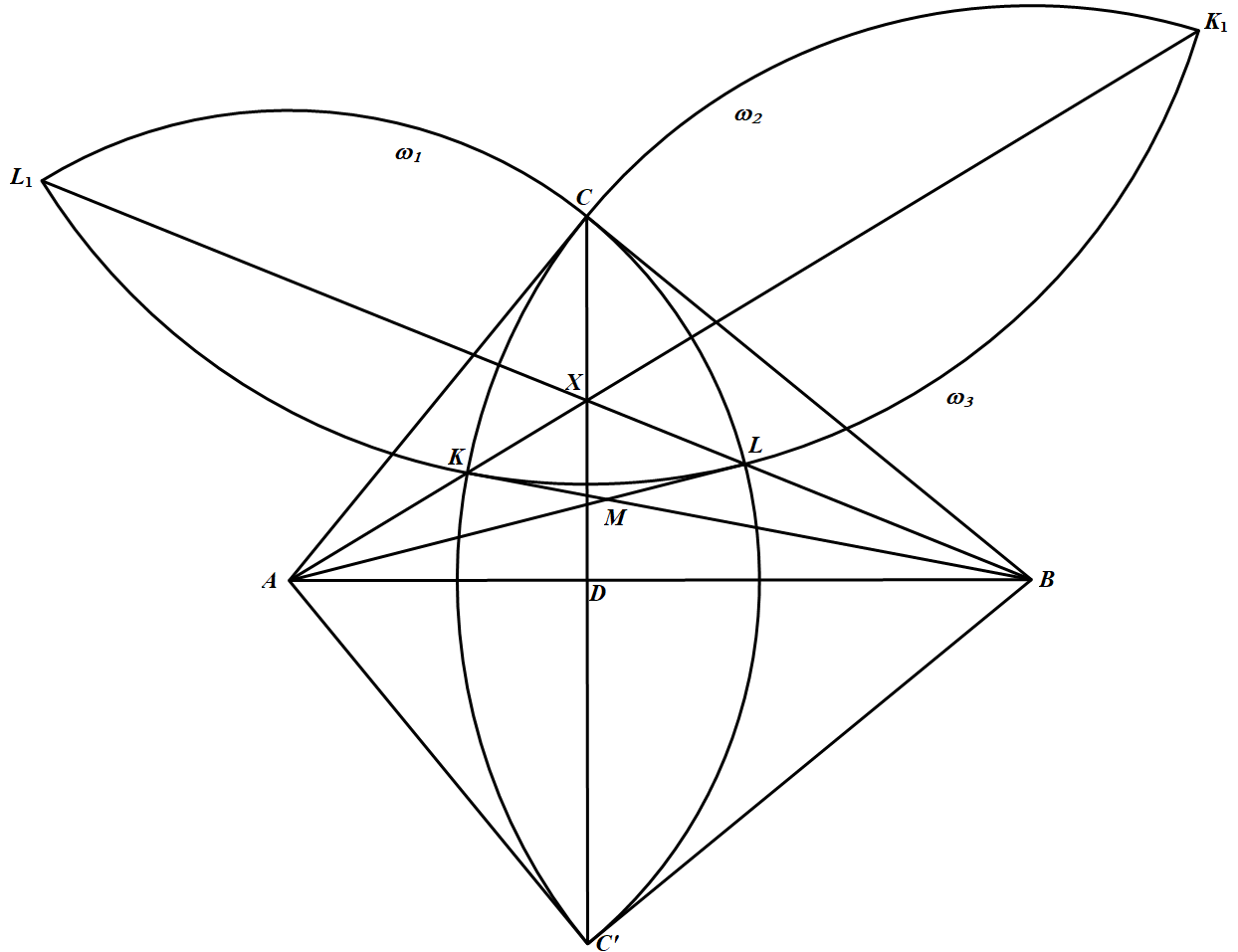
由圆幂定理可得 $XK\cdot XK_1=XC\cdot XC^\prime=XL\cdot XL_1$
所以，$K_1,L,K,L_1$ 四点共圆，记这个为 $\omega_3$．
对圆 $\omega_2$ 用圆幂定理得 $AL^2=AC^2=AK\cdot AK_1$，这说明直线 $AL$ 与圆 $\omega_3$ 相切于点 $L$．同理，直线 $BK$ 与圆 $\omega_3$ 相切于点 $K$．
于是 $MK$ 和 $ML$ 是从点 $M$ 到圆 $\omega_3$ 的两条切线，所以 $MK=ML$．
由圆幂定理可得 $XK\cdot XK_1=XC\cdot XC^\prime=XL\cdot XL_1$所以，$K_1,L,K,L_1$ 四点共圆，记这个为 $\omega_3$．
对圆 $\omega_2$ 用圆幂定理得 $AL^2=AC^2=AK\cdot AK_1$，这说明直线 $AL$ 与圆 $\omega_3$ 相切于点 $L$．同理，直线 $BK$ 与圆 $\omega_3$ 相切于点 $K$．
于是 $MK$ 和 $ML$ 是从点 $M$ 到圆 $\omega_3$ 的两条切线，所以 $MK=ML$．
答案
解析
备注
