设三角形 $ABC$ 的内心是 $I$，外接圆为 $\Gamma$．直线 $AI$ 交圆 $\Gamma$ 于另一点 $D$．设 $E$ 是弧 $\overparen{BDC}$ 上的一点，$F$ 是边 $BC$ 上的一点，使得 $\angle BAF=\angle CAE<\dfrac{1}{2}\angle BAC$．
设 $G$ 是线段 $IF$ 的中点．证明：直线 $DG$ 与 $EI$ 的交点在圆 $\Gamma$ 上．（中国香港）
设 $G$ 是线段 $IF$ 的中点．证明：直线 $DG$ 与 $EI$ 的交点在圆 $\Gamma$ 上．（中国香港）
【难度】
【出处】
2010年第51届IMO试题
【标注】
【答案】
略
【解析】
设 $I_a$ 是三角形 $ABC$ 边 $BC$ 上的旁切圆圆心，则 $D$ 是线段 $II_a$ 的中点，于是 $DG\parallel I_aF,\angle GDA=\angle FI_aA$．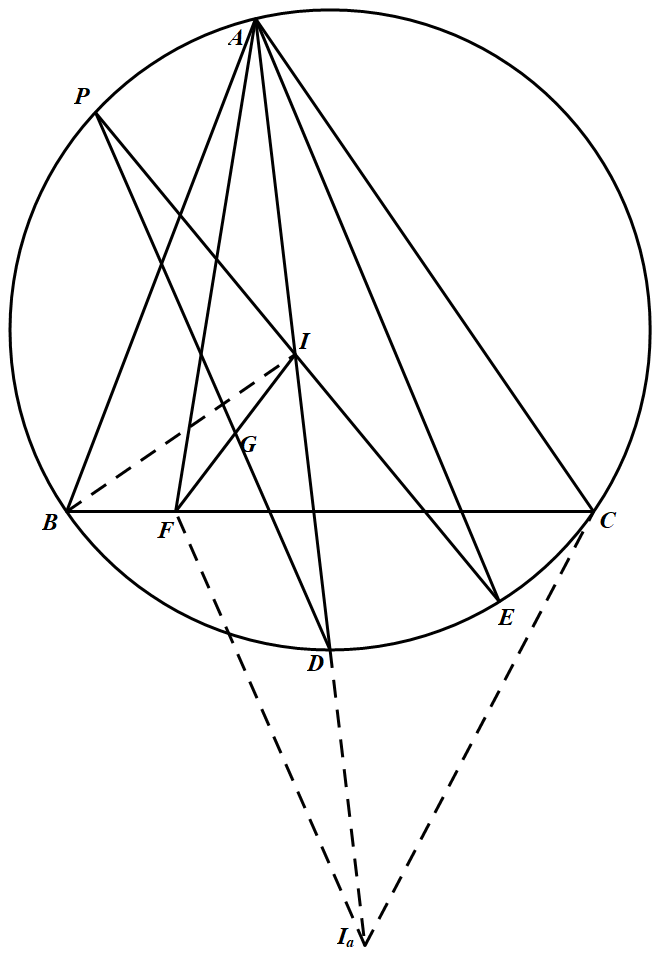
欲证直线 $DG$ 与 $EI$ 的交点 $P$ 在圆 $\Gamma$ 上，即证明 $A,E,D,P$ 四点共圆，等价于证明 $\angle GDA=\angle IEA$，也就是证明 $\angle FI_aA=\angle IEA$．
由题设 $\angle BAF=\angle CAE$，可得 $\triangle ABF\sim\triangle AEC$，所以
$\dfrac{AF}{AB}=\dfrac{AC}{AE}$ ①
由
$\angle AIB=\angle C+\dfrac{1}{2}(\angle A+\angle B)$
$\angle ACI_a=\angle C+\dfrac{1}{2}(\angle A+\angle B)$
可得 $\triangle ABI\sim\triangle AI_aC$
所以 $\dfrac{AI}{AB}=\dfrac{AC}{AI_a}$ ②
从 ①② 得 $\dfrac{AF}{AI}=\dfrac{AI_a}{AE}$ ③
由题设可知，$\angle FAI_a=\angle EAI$，所以 $\triangle AFI_a\sim \triangle AIE$，故 $\angle FI_aA=\angle IEA$．
欲证直线 $DG$ 与 $EI$ 的交点 $P$ 在圆 $\Gamma$ 上，即证明 $A,E,D,P$ 四点共圆，等价于证明 $\angle GDA=\angle IEA$，也就是证明 $\angle FI_aA=\angle IEA$．由题设 $\angle BAF=\angle CAE$，可得 $\triangle ABF\sim\triangle AEC$，所以
$\dfrac{AF}{AB}=\dfrac{AC}{AE}$ ①
由
$\angle AIB=\angle C+\dfrac{1}{2}(\angle A+\angle B)$
$\angle ACI_a=\angle C+\dfrac{1}{2}(\angle A+\angle B)$
可得 $\triangle ABI\sim\triangle AI_aC$
所以 $\dfrac{AI}{AB}=\dfrac{AC}{AI_a}$ ②
从 ①② 得 $\dfrac{AF}{AI}=\dfrac{AI_a}{AE}$ ③
由题设可知，$\angle FAI_a=\angle EAI$，所以 $\triangle AFI_a\sim \triangle AIE$，故 $\angle FI_aA=\angle IEA$．
答案
解析
备注
