设 $ABCD$ 是一个圆内接四边形，点 $P,Q$ 和 $R$ 分别是 $D$ 到直线 $BC$、$CA$ 和 $AB$ 的射影．求证：$PQ=QR$ 的充要条件是 $\angle ABC$ 和 $\angle CDA$ 的角平分线的交点在 $AC$ 上．（芬兰）
【难度】
【出处】
2003年第44届IMO试题
【标注】
【答案】
略
【解析】
证法一
欲证结论，这等价于证明
$\dfrac{AB}{BC}=\dfrac{AD}{CD}$．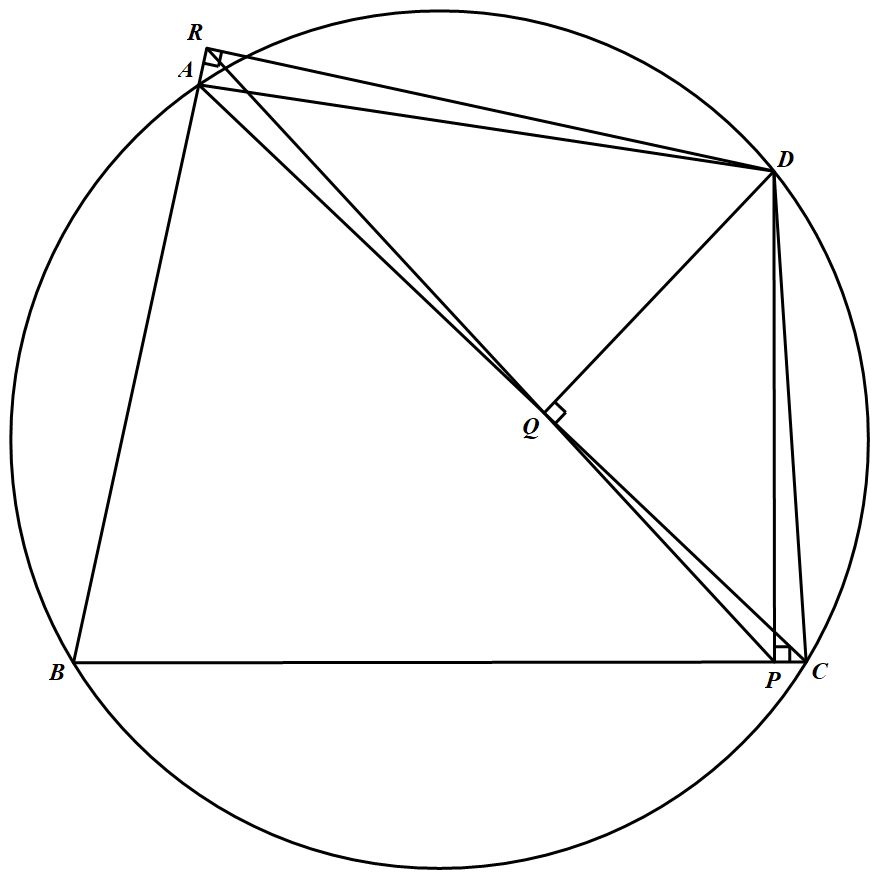
由 $A,R,D,Q$ 共圆，$C,P,Q,D$ 共圆及正弦定理，得
$\begin{aligned}
\frac{AB}{BC}&=\frac{\sin\angle ACB}{\sin\angle BAC}\\
&=\frac{\sin\angle QDP}{\sin\angle RDQ}\\
&=\frac{\frac{QP}{CD}}{\frac{QR}{AD}}\\
&=\frac{AD}{CD}\cdot\frac{PQ}{QR}
\end{aligned}$
于是 $\dfrac{AB}{BC}=\dfrac{AD}{CD}\Leftrightarrow PQ=QR$
注意 $A,B,C,D$ 共圆这一条件多余．
证法二
由Simson定理，可知 $P,Q,R$ 三点共线．而 $\angle DPC=\angle DQC=90^\circ$，故 $D,P,C,Q$ 四点共圆，于是，$\angle DCA=\angle DPQ=\angle DPR$．类似地，由于 $D,Q,R,A$ 共圆，可知 $\angle DAC=\angle DRP$．因此，$\triangle DCA\sim\triangle DPR$．
类似地 $\triangle DAB\sim\triangle DQP,\triangle DBC\sim\triangle DCRQ$．因此
$\dfrac{DA}{DC}=\dfrac{DR}{DP}=\dfrac{DB\cdot\frac{QR}{BC}}{DB\cdot\frac{PQ}{BA}}=\dfrac{QR}{PQ}\cdot \dfrac{BA}{BC}$
从而 $PQ=QR$ 的充要条件是 $\dfrac{DA}{DC}=\dfrac{BA}{BC}$．
欲证结论，这等价于证明
$\dfrac{AB}{BC}=\dfrac{AD}{CD}$．
由 $A,R,D,Q$ 共圆，$C,P,Q,D$ 共圆及正弦定理，得$\begin{aligned}
\frac{AB}{BC}&=\frac{\sin\angle ACB}{\sin\angle BAC}\\
&=\frac{\sin\angle QDP}{\sin\angle RDQ}\\
&=\frac{\frac{QP}{CD}}{\frac{QR}{AD}}\\
&=\frac{AD}{CD}\cdot\frac{PQ}{QR}
\end{aligned}$
于是 $\dfrac{AB}{BC}=\dfrac{AD}{CD}\Leftrightarrow PQ=QR$
注意 $A,B,C,D$ 共圆这一条件多余．
证法二
由Simson定理，可知 $P,Q,R$ 三点共线．而 $\angle DPC=\angle DQC=90^\circ$，故 $D,P,C,Q$ 四点共圆，于是，$\angle DCA=\angle DPQ=\angle DPR$．类似地，由于 $D,Q,R,A$ 共圆，可知 $\angle DAC=\angle DRP$．因此，$\triangle DCA\sim\triangle DPR$．
类似地 $\triangle DAB\sim\triangle DQP,\triangle DBC\sim\triangle DCRQ$．因此
$\dfrac{DA}{DC}=\dfrac{DR}{DP}=\dfrac{DB\cdot\frac{QR}{BC}}{DB\cdot\frac{PQ}{BA}}=\dfrac{QR}{PQ}\cdot \dfrac{BA}{BC}$
从而 $PQ=QR$ 的充要条件是 $\dfrac{DA}{DC}=\dfrac{BA}{BC}$．
答案
解析
备注
