查看数据源：5c85ed8d210b28428f14d46f
给定凸四边形 $ABCD$，$BC=DA$，且 $BC$ 不平行 $AD$．设点 $E$ 和 $F$ 分别在边 $BC$ 和 $AD$ 的内部，满足 $BE=DF$．直线 $AC$ 和 $BD$ 相 交于点 $P$，直线 $BD$ 和 $EF$ 相 交于点 $Q$，直线 $EF$ 和 $AC$ 相交于点 $R$．证明：当点 $E$ 和 $F$ 变动时，三角形 $PQR$ 的外接圆经过除 点 $P$ 外的另一个定点．（波兰）
【难度】
【出处】
2005年第46届IMO试题
【标注】
  • 知识点
    >
    二试几何部分
【答案】
略
【解析】
由题意，$BC$ 不平行于 $AD$，则三角形 $APD$ 的外接圆与三角形 $BPC$ 的外接圆不相切．否则，过切点作公切线 $SS^\prime$，则
$\angle DPS=\angle DAP,\angle BPS^\prime =\angle BCP$
又 $\angle DPS=\angle BPS^\prime$，所以 $\angle BCP=\angle DAP$，于是 $AD\parallel BC$，与题设矛盾．
故可设它们除点 $P$ 外交于点 $O$，则 $O$ 是定点．不妨设 $O$ 在三角形 $DPC$ 内，下面证明：当点 $E$ 和 $F$ 变动时，三角形 $PQR$ 的外接圆经过点 $O$．
如图所示，连接 $OA,OB,OC,OD,OE,OF,OP,OQ,OR$，则由 $B,C,O,P$ 四点共圆和 $O,P,A,D$ 四点共圆得：
$\angle OBC=\angle OPC,\angle OPC=\angle ADO$
所以 $\angle OBC=\angle ADO$．同理
$\angle OCB=\angle DPO=\angle DAO$．
再结合 $AD=BC$，得 $\triangle OBC\cong ODA$，故
$OB=OD,\angle OBE=\angle ODF$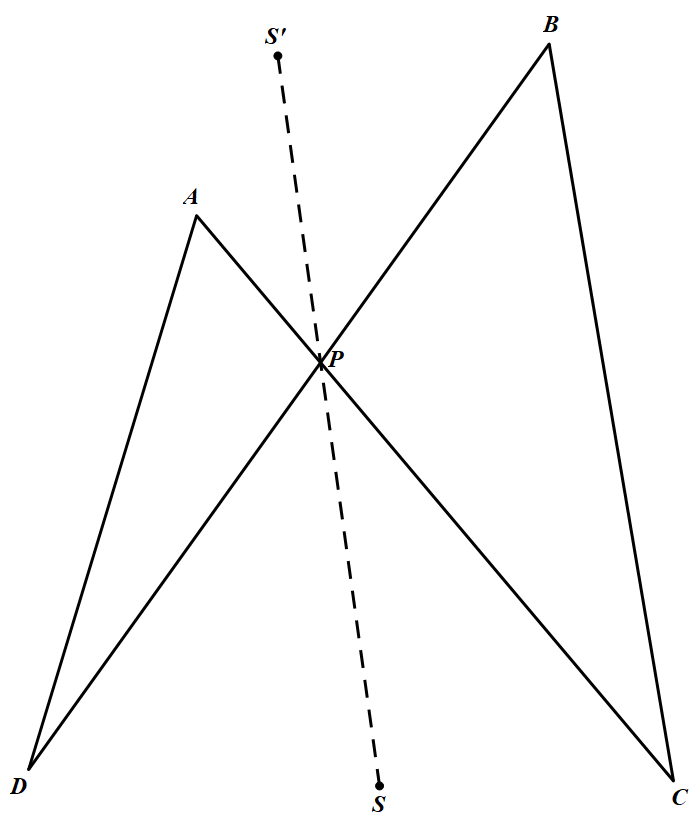．又由条件 $BE=DF$ 可得，$\triangle OBE\cong\triangle ODF$，所以 $OE=OF,OB=OD$．而
$\angle FOE=\angle FOB+\angle BOE=\angle BOF+\angle FOD=\angle BOD$
于是 $\triangle BOD\sim\triangle FOE$，所以 $\angle EFO=\angle BDO$，即 $\angle QFO=\angle QDO$，因此 $Q,F,D,O$ 四点共圆，得 $\angle RQO=\angle FDO$．而 $O,P,A,D$ 四点共圆，故 $\angle FDO=\angle ADO=\angle RPO$
因而 $\angle RQO=\angle RPO$，所以 $O,R,P,Q$ 四点共圆．
综上所述，当点 $E$ 和 $F$ 变动时，三角形 $PQR$ 的外接圆经过除 $P$ 外的另一个定点 $O$．
答案 解析 备注
0.159307s