重置
序号 ID 年级 类型 来源 摘要 创建时间
15123 5cd0fce2210b28021fc75eca 高中 解答题 自招竞赛 $\triangle ABC$ 中，$A,B,C$ 所对的边分别为 $a,b,c,\tan C=\dfrac{\sin A+\sin B}{\cos A+\cos B},\sin(B-A)=\cos C$． 2022-04-17 19:47:10
15041 5f000478210b28774f712eb6 高中 解答题 高中习题 已知 $\frac{1-\tan\theta}{2+\tan\theta}=1$，求证：$\tan2\theta=-4\tan\left(\theta+\frac{\pi}{4}\right).$ 2022-04-17 19:03:10
15040 5f0005ca210b28774f712ebe 高中 解答题 高中习题 在 $\triangle ABC$ 中，已知 $\tan A,\tan B$ 是 $x$ 的方程 $x^2+p(x+1)+1=0$ 的两个实根，求 $\angle C.$ 2022-04-17 19:02:10
15039 5f0144d6210b28774f712f0a 高中 解答题 高中习题 已知 $\sin\frac{\alpha}{2}-\cos\frac{\alpha}{2}=\frac{1}{5}$，求 $\sin\alpha$ 的值； 2022-04-17 19:02:10
14994 603efe5725bdad000ac4d7f8 高中 解答题 自招竞赛 已知复数 $z_1,z_2,z_3$ 的辐角分别为 $\alpha, \beta, \gamma$，且 $|z_1|=1, |z_2|+|z_3|=2, z_1+z_2+z_3=0$．试求 $\cos(\alpha-\beta)+2\cos(\beta-\gamma)+3\cos (\gamma-\alpha)$ 的取值范围． 2022-04-17 19:37:09
14963 621df746ea59ab000a73d59d 高中 解答题 高中习题 若函数 $f(x)=\frac{1}{2}(\cos x-\sin x)(\cos x-\sin x)+3a(\sin x-\cos x)+(4a-1)x$ 在区间 $\left[-\frac{\pi}{4},0\right]$ 上单调递减，求实数 $a$ 的取值范围是． 2022-04-17 19:21:09
14962 621df76dea59ab000a73d5a2 高中 解答题 高中习题 解方程：$[\tan x]=2\sin^2x$． 2022-04-17 19:20:09
14941 622f2082ea59ab000a73d76d 高中 解答题 高中习题 设函数 $f(x)=\sin x, x\in \mathbb{R}. $ 2022-04-17 19:08:09
14932 622f1b05ea59ab000a73d764 高中 解答题 高中习题 已知 $f(\alpha )=\dfrac{\sin (3\pi-\alpha)\cos (5\pi+\alpha)}{\cos ^2 (\dfrac{3\pi}{2}-\alpha)+\sin ^2 (\dfrac{\pi}{2}+\alpha)}$． 2022-04-17 19:04:09
14931 622f1ff6ea59ab0009118a96 高中 解答题 高中习题 已知函数 $f(x)=2\sin(2x-\dfrac{\pi}{3})$，将 $f(x)$ 的图像向左平移 $t(\dfrac{\pi}{2}<t<\pi )$ 个单位长度，得到函数 $g(x)$ 的图像． 2022-04-17 19:03:09
14930 62303e34ea59ab0009118aac 高中 解答题 高中习题 已知函数 $ f(x)=\sqrt{3}\sin(\omega x-\dfrac{\pi}{6})(\omega >0) $ 的图象的相邻两条对称轴间的距离为 $ \dfrac{\pi}{2}$． 2022-04-17 19:02:09
14928 62303eacea59ab000a73d7c3 高中 解答题 高中习题 已知函数 $f(x)=A\sin(\omega x+\varphi)(A>0, \omega>0, -\dfrac{\pi}{2}＜\varphi＜\dfrac{\pi}{2}, x\in \mathbb{R})$ 的部分图象如图所示． 2022-04-17 19:01:09
14926 62303fc9ea59ab000a73d7c9 高中 解答题 高中习题 已知函数 $f(x)=A\sin(\omega x+\varphi )(x\in \mathbb{R}, A>0, \omega >0, 0<\varphi<\dfrac{\pi}{2})$ 的部分图象如图所示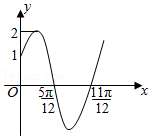． 2022-04-17 19:00:09
14925 62304324ea59ab000a73d7d1 高中 解答题 高中习题 函数 $ f(x)=A\sin(\omega x+\varphi)(A>0, \omega>0, |\varphi|<\dfrac{\pi}{2}, x\in \mathbb{R})$ 的部分图象如图，$M$ 是图象的一个最低点，图象与 $x$ 轴的一个交点的坐标为 $ (\dfrac{\pi}{2}, 0)$，与 $y$ 轴的交点坐标为 $ (0, -\sqrt{2})$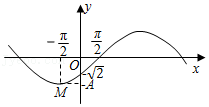． 2022-04-17 19:59:08
14900 601f8f5a25bdad0009f74030 高中 解答题 自招竞赛 设 $a\in\mathbb{R}, \theta\in[0,2\pi)$，复数 $z_1=\cos\theta+i\sin\theta, z_2=\sin\theta+i\cos\theta, z_3=a(1-i)$，试求所有的数对 $(a,\theta)$，使得 $z_1,z_2,z_3$ 依次成等比数列． 2022-04-17 19:46:08
14892 6231be1aea59ab000a73d94b 高中 解答题 高中习题 已知 $ \overrightarrow{m}=(\sin \omega x+\cos \omega x, \sqrt{3}\cos \omega x), \overrightarrow{n}=(\cos \omega x-\sin \omega x, 2\sin \omega x )(\omega>0)$，若 $f(x)=\overrightarrow{m}\cdot \overrightarrow{n}$，且 $f(x)$ 的图像相邻的对称轴间的距离不小于 $ \dfrac{\pi}{2}$． 2022-04-17 19:42:08
14891 6231bee3ea59ab000a73d958 高中 解答题 高中习题 已知 $ \dfrac{\pi}{4}<\alpha<\dfrac{\pi}{2} $，化简：$ \sqrt{2+2\cos 2\alpha}+\sqrt{1-\sin 2\alpha}-\sqrt{1+\sin 2\alpha}$； 2022-04-17 19:42:08
14890 6231bfd5ea59ab000a73d95f 高中 解答题 高中习题 ； 2022-04-17 19:42:08
14889 6231c031ea59ab000a73d969 高中 解答题 高中习题 已知 $ \theta$ 为第三象限角，化简 $ \sqrt{\dfrac{1+\cos \theta}{1-\cos \theta}}+\sqrt{\dfrac{1-\cos \theta}{1+\cos \theta}}$； 2022-04-17 19:41:08
14888 6231c083ea59ab0009118bae 高中 解答题 高中习题 已知函数 $f(x)=2\sqrt{3}\sin x\sin (\dfrac{\pi}{2}-x)-2\cos ^2x+1$． 2022-04-17 19:40:08
0.209768s