函数 $ f(x)=A\sin(\omega x+\varphi)(A>0, \omega>0, |\varphi|<\dfrac{\pi}{2}, x\in \mathbb{R})$ 的部分图象如图,$M$ 是图象的一个最低点,图象与 $x$ 轴的一个交点的坐标为 $ (\dfrac{\pi}{2}, 0)$,与 $y$ 轴的交点坐标为 $ (0, -\sqrt{2})$.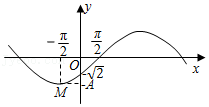
【难度】
【出处】
无
【标注】
-
(Ⅰ)求 $A, \omega , \varphi $ 的值;标注答案(Ⅰ)$ A=2, \omega=\dfrac{1}{2}, \phi=-\dfrac{\pi}{4}$解析略
-
(Ⅱ)若关于 $x$ 的方程 $f(x)-m=0$ 在 $[0, 2\pi]$ 上有一解,求实数 $m$ 的取值范围.标注答案(Ⅱ)$m$ 的取值范围是 $ m\in [-\sqrt{2}, \sqrt{2})\cup \{2\}$解析略
题目
问题1
答案1
解析1
备注1
问题2
答案2
解析2
备注2