重置
序号 ID 年级 类型 来源 摘要 创建时间
21973 5909869539f91d0008f05052 高中 解答题 自招竞赛 已知周六的降雨概率为 $40 \%$，周日的降雨概率为 $30 \%$，周六降雨的条件下周日降雨概率是周六不降雨的条件下周日降雨概率的 $2$ 倍．设周六周日两天至少有一天下雨的概率为 $\dfrac{a}{b} $，其中 $a,b$ 为互质的正整数．求 $a+b$ 的值． 2022-04-17 20:54:13
21958 590a8f796cddca000a081892 高中 解答题 高中习题 袋中共有 $3n$ 个小球，红、绿、蓝各 $n$ 个．现从袋中随机取球，每次取出 $3$ 个小球不放回，直至某种颜色的小球被全部取出，求取球次数 $X$ 的分布列． 2022-04-17 20:44:13
21923 5a4b481d34d6f90007a584cd 高中 解答题 自招竞赛 求满足以下条件的正整数数列 $\{a_n\}$（$n\in\mathbb N$）的个数：对任意 $n\in\mathbb N$ 都有 $a_n\leqslant 100$ 且 $a_n=a_{n+100}$ 且 $a_n\ne a_{n+1}$． 2022-04-17 20:26:13
21614 59546703d3b4f9000ad5e7d0 高中 解答题 高中习题 游戏规则如下：如果某次随机地投掷出手中的骰子后有 $2$ 颗骰子的点数之和为 $7$，则获胜．现在手中恰好有 $2$ 颗骰子，有两种奖励（bonus）可以领取：
奖励A，额外的 $2$ 次投掷机会；
奖励B，额外的 $1$ 颗骰子．		 2022-04-17 20:35:10
21610 5908233c060a05000bf29143 高中 解答题 高中习题 若甲乙对局时，甲赢得单局比赛的概率为 $p$（$p>0.5$），求证：在 $2n+1$ 局 $n+1$ 胜（如 $5$ 局 $3$ 胜）制的比赛中，甲最终胜出的概率随着 $n$ 的增大而增大． 2022-04-17 20:33:10
21572 595c8fc46e0c650007a042af 高中 解答题 高中习题 有 $7$ 个编号分别为 $1,2,3,4,5,6,7$ 的小球，其中编号为 $1,2$ 的小球为红色，编号为 $3,4$ 的小球为黑色，编号为 $5,6,7$ 的小球为白色，将这些小球放入 $5$ 个不同的盒子中，每个盒子放 $1$ 个或 $2$ 个小球，同色球不能放在同一个盒子里，求不同的放置方法总数． 2022-04-17 20:12:10
21359 595c586a866eeb000a0355db 高中 解答题 高考真题 某高校数学系计划在周六和周日各举行一次主题不同的心理测试活动，分别由李老师和张老师负责．已知该系共有 $n$ 位学生，每次活动均需该系 $k$ 位学生参加（$n$ 和 $k$ 都是固定的正整数）．假设李老师和张老师分别将各自活动通知的信息独立、随机地发给该系 $k$ 位学生，且所发信息都能收到．记该系收到李老师或张老师所发活动通知信息的学生人数为 $X$． 2022-04-17 20:13:08
21340 590c21ec857b42000aca37d0 高中 解答题 高中习题 游戏规则如下：如果某次随机地投掷出手中的骰子后有 $2$ 颗骰子的点数之和为 $7$，则获胜．现在手中恰好有 $2$ 颗骰子，但有两种奖励（bonus）可以领取，请问选择哪种奖励获胜的几率大？
奖励A，额外的 $2$ 次投掷机会；
奖励B，额外的 $1$ 颗骰子．		 2022-04-17 20:06:08
21338 5966f1de030398000abf1531 高中 解答题 自招竞赛 试确定，有多少种不同的方法将集合 $M=\{1,2,3,4,5\}$ 中的元素归入 $A,B,C$ 三个（有序）集合，使得满足：每个元素至少含于其中一个集合之中，这三个集合的交集是空集，而其中任两个集合的交都不是空集？（即 $A\cup B\cup C=M$，$A\cap B\cap C=\varnothing$，而 $A\cap B\ne \varnothing$，$B\cap C\ne\varnothing$，$C\cap A\ne\varnothing$） 2022-04-17 20:04:08
21142 5c6a5b58210b281dbaa9341f 高中 解答题 自招竞赛 一种商业用的带10个按钮的锁，只要按了正确的5个数字的按钮，而不管顺序如何，就可以打开．如图是用 $\left\{ 1 2 3 6 9 \right\}$ 作为它的组合的例子．假如重新设计这些锁，使1个数字按钮到9个数字按钮都可以作为开锁的组合，问还可以有多少种另外的组合（即不是用5个数码控制的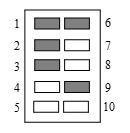）？ 2022-04-17 20:17:06
21136 5c6a219f210b281dbaa93309 高中 解答题 自招竞赛 亚瑟王的25位骑士坐在他们的圆桌旁，选出3位骑士（选择哪三个，都是等概率的）去斩妖龙．设 $P$ 是选出的3位之中至少有两位座次相邻的概率．如果 $P$ 写成既约分数，求分子与分母的和． 2022-04-17 20:14:06
21134 5c6a21e0210b281db9f4c6de 高中 解答题 自招竞赛 1447，1005，1231这几个数有许多共同之处：它们都是四位数，最高位是1，都恰有两个相同的数字，一共有多少个这样的数？ 2022-04-17 20:13:06
21126 5c6a3eaf210b281dbaa9333c 高中 解答题 自招竞赛 设 $S$ 是一张由正整数（可以重复出现）组成的表，表中包含数68．$S$ 中的各数的算术平均值是56．但是，如果把68去掉，剩下的各数算术平均值就降为55．问可能在 $S$ 中出现的最大数是多少？ 2022-04-17 20:08:06
21107 5c6a4e98210b281db9f4c780 高中 解答题 自招竞赛 在扔硬币时，如果用Z且示正面朝上，F表示反面朝上，那么扔硬币的序列就表示为用Z和F组成的串，我们可以统计在这种序列中正面紧跟着反面 $\left( \text{FZ} \right)$ 的出现次数，正面紧跟着正面 $\left( \text{ZZ} \right)$ 的出现次数……例如，序列ZZFFZZZZFZZFFFF是15次扔硬币的结果，其中有5个ZZ，3个ZF，2个FZ，4个FF．问有多少个15次扔硬币的序列，恰好有2个ZZ，3个ZF，4个FZ，5个FF？ 2022-04-17 20:58:05
21084 5c6a5f09210b281dbaa93442 高中 解答题 自招竞赛 老板将要打印的信件交给秘书，每次给一封，且放在信堆的最上面，秘书一有空就从最上面拿一封信来打，有一天共有9封信要打，老板按第一封、第二封、…、第九封的顺序交给秘书．午饭的时候，秘书告诉同事，已把第八封信打好了，但未透露上午工作的其他情况．这个同事很想知道还剩下哪些信件没有打，还想知道按什么样的顺序来打印．
根据以上的信息，下午打的信的顺序有多少种可能（没有要打的信也是一种可能）？		 2022-04-17 20:43:05
21082 5c6a7491210b281db9f4c807 高中 解答题 自招竞赛 10个点标记在圆周上，以这10个点中的某些点或者全部的点为顶点，能画得多少个不同的三角形或者凸多边形（两个多边形除非它们有完全相同的顶点，否则都是不同的）？ 2022-04-17 20:43:05
21079 5c6a749f210b281db9f4c811 高中 解答题 自招竞赛 某个不均匀的硬币被抛掷5次，恰好出现1次正面的概率不等于0，且等于恰好出现2次正面的概率，设既约分数 $\frac{i}{j}$ 是5次中恰好出现3次正面的概率，求 $i+j$． 2022-04-17 20:40:05
21074 5c6a74c3210b281db9f4c829 高中 解答题 自招竞赛 给出由121个整数组成的一个样本（即这些整数组成的一个集合），这些整数在1～1000（包括1和1000）允许重复出现，这个样本中有唯一的众数（即出现次数最多的数），设 $D$ 为众数与样本的算术平均值之差．
若让 $D$ 尽可能大，$\left[ D \right]$ 是多少（对实数 $x$，$\left[ x \right]$ 是小于或等于 $x$ 的最大的整数）？		 2022-04-17 20:38:05
21073 5c6a74d6210b281db9f4c835 高中 解答题 自招竞赛 给定一个正整数 $n$，能够证明每个形如 $r+s\text{i}$ 的复数（$r$，$s$ 为整数）能用整数0，1，2，…，${{n}^{2}}$ 作为“数码”唯一地表示成“$-n+\text{i}$ 进位制”的形式，即方程
$r+s\text{i}={{a}_{m}}{{\left( -n+\text{i} \right)}^{m}}+{{a}_{m-1}}{{\left( -n+\text{i} \right)}^{m-1}}+\cdots +{{a}_{1}}\left( -n+\text{i} \right)+{{a}_{0}}$ 对于唯一地选取的非负整数 $m$ 与数码 ${{a}_{0}}$，${{a}_{1}}$，…，${{a}_{m}}$（它们取自集合 $\left\{ 0 1 2 \cdots {{n}^{2}} \right\}$，${{a}_{m}}\ne 0$）成立．这时以 $r+s\text{i}={{\left( {{a}_{m}}{{a}_{m-1}}\cdots {{a}_{1}}{{a}_{0}} \right)}_{-n+\text{i}}}$ 记为 $r+s\text{i}$ 的“$-n+\text{i}$ 进位制”展开式．只有有限多个整数 $k+0\text{i}$ 具有“四位数”展开式，$k={{\left( {{a}_{3}}{{a}_{2}}{{a}_{1}}{{a}_{0}} \right)}_{-3+\text{i}}}$，${{a}_{3}}\ne 0$．求全部这种 $k$ 的和．		 2022-04-17 20:38:05
21065 5c6b70bc210b281db9f4c869 高中 解答题 自招竞赛 在一次射击比赛中，8个泥制的靶子挂成三列，其中两列各挂3个，一列挂2个，如图所示．一射手按照下列规则去击碎靶子，先挑选一列，然后必须击碎这列中尚未被击碎的靶子中最低的一个，若每次射击都遵循这一规则，击碎全部8个靶子可以有多少种不同的次序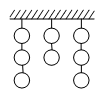？ 2022-04-17 20:33:05
0.185644s