一种商业用的带10个按钮的锁,只要按了正确的5个数字的按钮,而不管顺序如何,就可以打开.如图是用 $\left\{ 1 2 3 6 9 \right\}$ 作为它的组合的例子.假如重新设计这些锁,使1个数字按钮到9个数字按钮都可以作为开锁的组合,问还可以有多少种另外的组合(即不是用5个数码控制的)?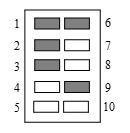

【难度】
【出处】
1988年第6届美国数学邀请赛(AIME)
【标注】
【答案】
770
【解析】
10个按钮可以有 ${{2}^{10}}$ 种选择方式,从中我们要除去10个数码都选上的及没有一个数码选上的,还要除去正好选择5个数码的情况.因此总数为
${{2}^{10}}-1-1-\text{C}_{10}^{5}=1024-2-252=770$.
${{2}^{10}}-1-1-\text{C}_{10}^{5}=1024-2-252=770$.
答案
解析
备注