试确定，有多少种不同的方法将集合 $M=\{1,2,3,4,5\}$ 中的元素归入 $A,B,C$ 三个（有序）集合，使得满足：每个元素至少含于其中一个集合之中，这三个集合的交集是空集，而其中任两个集合的交都不是空集？（即 $A\cup B\cup C=M$，$A\cap B\cap C=\varnothing$，而 $A\cap B\ne \varnothing$，$B\cap C\ne\varnothing$，$C\cap A\ne\varnothing$）
【难度】
【出处】
2012年全国高中数学联赛山西省预赛
【标注】
【答案】
$1230$
【解析】
如图考虑 $\mathrm{Venn}$ 图所分成的七个部分，分别用 $x,u,v,w,a,b,c$ 表示．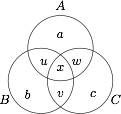
现将 $M$ 的元素填入各个部分中，据题意知，$x$ 处不能填数，而 $u,v,w$ 处必须填有数字，且所填元素互不相同（否则相同元素将归入 $x$ 区域中）；$a,b,c$ 处可以填写或不填写数字，但不能填有相同元素，（否则又将归入 $u,v,w$ 中）．
今用 $\overline{u}$ 表示 $u$ 处所填数字的个数，其余类推．
根据对称性，不妨按 $\overline{u}\leqslant\overline{v}\leqslant\overline{w}$ 的情况列举，则有四种情况：\[\begin{split}(\overline{u},\overline{v},\overline{w})=(1,1,1)\\
(\overline{u},\overline{v},\overline{w})=(1,1,2)\\
(\overline{u},\overline{v},\overline{w})=(1,2,2)\\
(\overline{u},\overline{v},\overline{w})=(1,1,3)\end{split}\]情形一 $(\overline{u},\overline{v},\overline{w})=(1,1,1)$．
从 $M$ 中各取一数分别置于 $u,v,w$ 处，有方法 $5\cdot4\cdot3=60$ 种，剩下两数各随意放入 $a,b,c$ 处，方法数为 $3^2$，于是相应的情况有 $60\cdot9=540$ 种．
情形二 $(\overline{u},\overline{v},\overline{w})=(1,1,2)$．
$u,v,w$ 中，含两个数的部分有 $3$ 种情况，对于其中任一情况，$M$ 中取两数放入一处，另外两处各方一数，有方法 $\mathrm{C}_5^2\mathrm{C}_3^1\mathrm{C}_2^1=60$ 种，剩下一数放于 $a,b,c$ 之一，有 $3$ 种方法，于是相应的情况有 $3\cdot60\cdot3=540$ 种．
情形三 $(\overline{u},\overline{v},\overline{w})=(1,2,2)$．
$u,v,w$ 中，含一个数的部分有 $3$ 种情况，对于其中任一情况，$M$ 中取一数放入一处，另外取两数方于一处，剩下两数放于另一处，有 $\mathrm{C}_5^1\mathrm{C}_4^2=30$ 种，共得 $3\cdot60\cdot3=540$ 种情况．
情形四 $(\overline{u},\overline{v},\overline{w})=(1,1,3)$．
$u,v,w$ 中，含三个数的部分有 $3$ 种情况，对于其中任一情况，$M$ 中取 $3$ 个数放入一处，另外的两处个放一个数，有 $\mathrm{C}_5^3\mathrm{C}_2^1=20$ 种，共得 $3\cdot20=60$ 种情况．
综合以上情形，总情况有 $540+540+90+60=1230$ 种，每种情况都获得满足条件的三个集合 $A,B,C$，因此结果为 $1230$．
现将 $M$ 的元素填入各个部分中，据题意知，$x$ 处不能填数，而 $u,v,w$ 处必须填有数字，且所填元素互不相同（否则相同元素将归入 $x$ 区域中）；$a,b,c$ 处可以填写或不填写数字，但不能填有相同元素，（否则又将归入 $u,v,w$ 中）．今用 $\overline{u}$ 表示 $u$ 处所填数字的个数，其余类推．
根据对称性，不妨按 $\overline{u}\leqslant\overline{v}\leqslant\overline{w}$ 的情况列举，则有四种情况：\[\begin{split}(\overline{u},\overline{v},\overline{w})=(1,1,1)\\
(\overline{u},\overline{v},\overline{w})=(1,1,2)\\
(\overline{u},\overline{v},\overline{w})=(1,2,2)\\
(\overline{u},\overline{v},\overline{w})=(1,1,3)\end{split}\]
从 $M$ 中各取一数分别置于 $u,v,w$ 处，有方法 $5\cdot4\cdot3=60$ 种，剩下两数各随意放入 $a,b,c$ 处，方法数为 $3^2$，于是相应的情况有 $60\cdot9=540$ 种．
$u,v,w$ 中，含两个数的部分有 $3$ 种情况，对于其中任一情况，$M$ 中取两数放入一处，另外两处各方一数，有方法 $\mathrm{C}_5^2\mathrm{C}_3^1\mathrm{C}_2^1=60$ 种，剩下一数放于 $a,b,c$ 之一，有 $3$ 种方法，于是相应的情况有 $3\cdot60\cdot3=540$ 种．
$u,v,w$ 中，含一个数的部分有 $3$ 种情况，对于其中任一情况，$M$ 中取一数放入一处，另外取两数方于一处，剩下两数放于另一处，有 $\mathrm{C}_5^1\mathrm{C}_4^2=30$ 种，共得 $3\cdot60\cdot3=540$ 种情况．
$u,v,w$ 中，含三个数的部分有 $3$ 种情况，对于其中任一情况，$M$ 中取 $3$ 个数放入一处，另外的两处个放一个数，有 $\mathrm{C}_5^3\mathrm{C}_2^1=20$ 种，共得 $3\cdot20=60$ 种情况．
综合以上情形，总情况有 $540+540+90+60=1230$ 种，每种情况都获得满足条件的三个集合 $A,B,C$，因此结果为 $1230$．
答案
解析
备注
