重置
序号 ID 年级 类型 来源 摘要 创建时间
15095 5d1097da210b280220ed4c02 高中 解答题 自招竞赛 如图，圆形的水池被分割为 $2n(n\geqslant 5)$ 个“格子”．我们把有公共隔墙（公共边或公共弧）的“格子”称为相邻的，从而每个“格子”都有三个邻格．
水池中一共跳人了 $4n+ 1$ 只青蛙，青蛙难于安静共处，只 要某个“格子”中有不少于 $3$ 只青蛙，那么迟早一定会有其中 $3$ 只分别同时跳往三个不同邻格．证明：只要经过一段时间之后，青蛙便会在水池中大致分布均匀．
所谓大致分布均匀，就是任取其中一个“格子”，或者它里面有青蛙，或者它的三个邻格里都有青蛙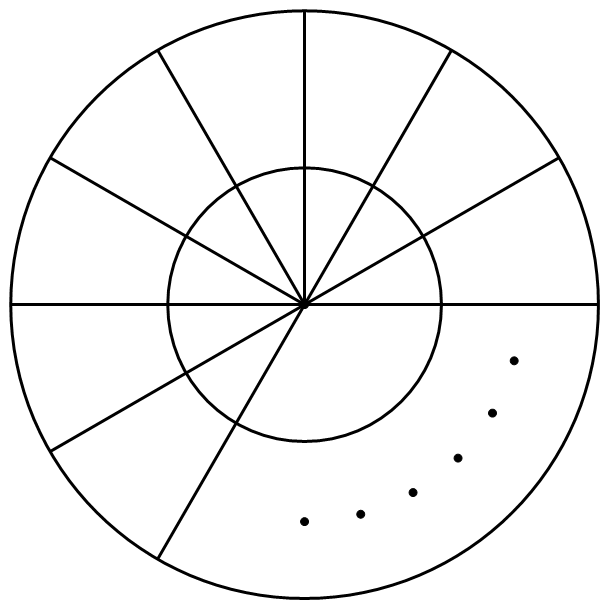．		 2022-04-17 19:33:10
15093 5d11b2a9210b280220ed4cd7 高中 解答题 自招竞赛 艾米和鲍勃在玩一个游戏。游戏一开始，艾米在黑板上写下一个正整数，之后两人轮流进行行动，鲍勃先开始。在鲍勃的轮次中，鲍勃会将黑板上的数字 $n$ 替换为 $n-a^2$，其中 $a$ 为正整数。在艾米的行动轮次中，她会将黑板上的数字 $n$ 替换为 $n^k$，其中 $k$ 为正整数。如果黑板上的数字变为零，则鲍勃获胜。提问艾米是否有策略来防止鲍勃获胜？（Russian Maxim Didin） 2022-04-17 19:32:10
15087 5d25c055210b28021fc7836d 高中 解答题 自招竞赛 给定正整数 $n\geqslant 2$，设方恪表
$A=\left[\begin{array}{cccc}{a_{11}} & {a_{12}} & {\cdots} & {a_{1 n}} \\ {a_{21}} & {a_{22}} & {\cdots} & {a_{2 n}} \\ {\vdots} & {\vdots} & {\cdots} & {\vdots} \\ {a_{n 1}} & {a_{n 2}} & {\cdots} & {a_{nn}}\end{array}\right]$ 和 $B=\left[\begin{array}{cccc}{b_{11}} & {b_{12}} & {\cdots} & {b_{1 n}} \\ {b_{21}} & {b_{22}} & {\cdots} & {b_{2 n}} \\ {\vdots} & {\vdots} & {\cdots} & {\vdots} \\ {b_{n 1}} & {b_{n 2}} & {\cdots} & {b_{n n}}\end{array}\right]$
满足 $\left\{a_{i j} | 1 \leqslant i, j \leqslant n\right\}=\left\{b_{i j} | 1 \leqslant i, j \leqslant n\right\}=\left\{1,2, \cdots, n^{2}\right\}$．对 $A$ 实行如下操作：选取位于同一行或同一列的某两个数，交换它们的位置，其余 $n^2-2$ 个数保持不动，称为一次对换．求最小正整数 $m$，使得对任意的 $A、B$，可以经过不超过 $m$ 次对换，把 $A$ 变成 $B$．		 2022-04-17 19:29:10
15077 5d3fb6ec210b280220ed6d1d 高中 解答题 自招竞赛 我们称 $A_{1}, A_{2}, \cdots, A_{n}$ 为集合的一个 $n$ 分划，如果
（1）$A_{1} \cup A_{2} \cup \cdots \cup A_{n}=A ;(2) A_{i} \cap A_{j}=\varnothing, 1 \leqslant i<j\leqslant n$．
求最小的正整数 $m$，使得对 $A=\{1,2, \cdots, m\}$ 的任意一个 $14$ 分划 $A_{1}, A_{2}, \cdots, A_{14}$，一定存在某个集合 $A_{i}(1 \leqslant i \leqslant 14)$，在 $A_i$ 中有两个元素 $a,b$ 满足 $b<a \leqslant\dfrac{4}{3} b$．		 2022-04-17 19:26:10
15076 5d3fe069210b280220ed6d8d 高中 解答题 自招竞赛 设 $n$ 是给定的不小于 $4$ 的偶数．在平面直角坐标系 $xOy$ 中，点集 $A=\{(x, y) | x, y \in\{1,2, \cdots, n\}\}$．将 $A$ 中的 $n^2$ 个点任意地配成 $\dfrac{n^2}{2}$ 对，每对两个点之间连一条直线（已有的直线不再重复作），用 $\Gamma$ 表示这些直线的全体，井用 $\alpha(\Gamma)$ 表示 $\Gamma$ 中任意两条直线的夹角的最大值．求 $\alpha(\Gamma)$ 的最小正值． 2022-04-17 19:25:10
15058 5e9d230d210b280d3611214f 高中 解答题 高中习题 某校羽毛球社团有 $n$ 名成员（$n\geqslant 3$），每个学期都需要打排名赛。排名赛采用单循环赛制，任意两名队员都需要单挑一场比赛分出胜负．如果在比赛中形成 $A$ 赢 $B$，$B$ 赢 $C$，$C$ 赢 $A$ 的情况，则称形成三人循环组．求一个学期排名赛中，三人循环组个数的最小值和最大值． 2022-04-17 19:14:10
15051 5ef2f2e6210b28017ae2f64b 高中 解答题 自招竞赛 空间中 $8$ 个点，其中任意四点不共面，在这些点之间连接 $17$ 条线段．证明：在这 $17$ 条线段之中必存在 $3$ 条线段，其长度 $a,b,c$ 满足不等式 $\frac{a^2+b^2+c^2}{4}\geqslant \sqrt{3p(p-a)(p-b)(p-c)}$，其中 $p=\frac{a+b+c}{2}$． 2022-04-17 19:10:10
15032 5f291e98210b2865a8643c80 高中 解答题 高中习题 六，是否存在正整数集合的 $100$ 个两两不交的子集 $A_1,A_2,\ldots ,A_{100}$ 满足：对任意无穷多个质数组成的集合 $S$，存在正整数 $m$ 以及$$a_1\in A_1, a_2\in A_2, \ldots a_{100}\in A_{100},$$使得 $a_1,a_2,\ldots,a_{100}$ 都可以表示为 $S$ 中的 $m$ 个不同质数的乘积． 2022-04-17 19:57:09
15022 5fffbb18210b28117636f9dc 高中 解答题 自招竞赛 已知素数 $p$．甲，乙轮流玩游戏：有 $p$ 个空盒排成一排，记每一次操作是当前的玩家放一个数码到其中一个空盒子内．甲先开始．游戏结束后，所有的盒子均放有数码，且得到一个 $p$ 位数 $M$，在这些数码中，允许放置数码零．若 $p~|~M$，则甲获胜；否则，乙获胜．证明：甲有获胜策略． 2022-04-17 19:53:09
15020 60013301210b281da1784b15 高中 解答题 自招竞赛 某公司有 $n$ 名员工，已知这 $n$ 名员工中的每两个人均能保证在每周至少有三天是其中一位工作而另一位不工作（这几天工作的不一定是同一位员工，并且员工可以一周都不上班）．求 $n$ 的最大值． 2022-04-17 19:51:09
15010 6011319525bdad0009f73e87 高中 解答题 自招竞赛 对整数 $n\geqslant 2$，设$$A=(a_{i,j})_{n\times n}=\left(\begin{array}{cccc}
a_{1,1} & a_{1,2} & \cdots&a_{1,n}\\
a_{2,1} & a_{2,2} & \cdots & a_{2,n}\\
\vdots&\vdots&\quad&\vdots\\
a_{n,1}&a_{n,2}&\cdots&a_{n,n}\\
\end{array} \right) $$是一个由 $1,2,\ldots , n^2$ 组成的 $n$ 行的数表（每个数恰好出现一次）．
若存在 $1\leqslant i\leqslant n, 1\leqslant j\leqslant n$，使得 $a_{i,j}$ 既是第 $i$ 行中的最大值，也是第 $j$ 列中的最小值，则称数表 $A$ 是一个 $n$ 阶好数表，$a_{i,j}$ 为数表 $A$ 的一个特征数．将所有的 $n$ 阶好数表构成的集合记为 $S_n$．		 2022-04-17 19:46:09
15006 601b686425bdad000ac4d3b6 高中 解答题 自招竞赛 给定空间中的 $n$ 个点，其中任意 $4$ 点不共面，将联结这 $n$ 个点的每条线段都染为红，蓝二色之一．试求最小的正整数 $n$，使得总存在两个单色三角形，它们恰有一个公共顶点．这里，所谓单色三角形，是指该三角形的三条边被染为同一种颜色． 2022-04-17 19:43:09
14998 602f5d1425bdad000ac4d5de 高中 解答题 高中习题 试求最大的正整数 $k$，使得可以将正十四边形的 $k$ 个顶点染成红色，并且以这些红点作为顶点的四边形，只要其中有两条边平行，就一定是矩形． 2022-04-17 19:40:09
14987 604ae83e95a31e00081c49e5 高中 解答题 自招竞赛 设整数 $n\geqslant 3$．一次数学竞赛共有 $3n$ 名参赛者，它们一共使用 $n$ 种语言进行交流，并且每个参赛者恰使用其中 $3$ 种语言．证明：可以从中选出 $\lceil\frac{2n}{9}\rceil$ 种语言，使得不存在参赛者使用其中超过两种语言． 2022-04-17 19:34:09
11681 590ad4746cddca0008610f0f 高中 填空题 自招竞赛 在边长为 $1$ 的正方形中（含边界）取 $9$ 个点，其中必有 $3$ 个点，它们构成的三角形面积不超过 $M$，则 $[100M]=$  ，其中 $[x]$ 表示不超过实数 $x$ 的最大整数． 2022-04-16 22:16:33
11677 590be0066cddca0008611031 高中 填空题 自招竞赛 已知非空集合 $A,B$ 满足 $A\cup B=\left\{1,2,3,\cdots,8\right\}$，$A\cap B=\varnothing$．若 $A$ 中元素的个数不是 $A$ 中的元素，$B$ 中元素的个数不是 $B$ 中的元素，则满足条件的所有不同的集合 $A$ 的个数为 ． 2022-04-16 22:14:33
11644 596339823cafba000ac43f8d 高中 填空题 自招竞赛 设 $A$ 是由任意 $100$ 个互不相同的正整数组成的集合，令 $B=\left\{\dfrac ab\mid a,b \in A ,a \neq b\right\}$，$f(A)$ 表示集合 $B$ 中元素的个数，则 $f(A)$ 的最大值与最小值之和为  ． 2022-04-16 22:56:32
11639 59644665e6a2e7000d504777 高中 填空题 自招竞赛 已知集合 $A$ 的元素都是整数，其中最小的为 $1$，最大的为 $200$，且除 $1$ 以外，$A$ 中每一个数都等于 $A$ 中某两个数（可以相同）的和．则 $|A|$ 的最小值为 ．（符号 $|A|$ 表示集合 $A$ 中元素的个数） 2022-04-16 22:53:32
11603 596c7e4222d14000081817ca 高中 填空题 自招竞赛 集合的容量是指集合中元素的和，则满足条件“$A \subseteq \{1,2,3,4,5,6,7\}$，且当 $a\in A$ 时，必有 $8-a \in A$”的所有非空集合 $A$ 的容量的总和是 ．（用具体数字作答） 2022-04-16 22:34:32
11587 597822aefcb236000b022bf3 高中 填空题 自招竞赛 将总和为 $200$ 的 $10$ 个数放置在给定的一个圆周上，且任意三个相邻的数之和不小于 $58$．所有满足上述要求的 $10$ 个数中最大数的最大值为  ． 2022-04-16 22:26:32
0.196363s