如图，圆形的水池被分割为 $2n(n\geqslant 5)$ 个“格子”．我们把有公共隔墙（公共边或公共弧）的“格子”称为相邻的，从而每个“格子”都有三个邻格．
水池中一共跳人了 $4n+ 1$ 只青蛙，青蛙难于安静共处，只 要某个“格子”中有不少于 $3$ 只青蛙，那么迟早一定会有其中 $3$ 只分别同时跳往三个不同邻格．证明：只要经过一段时间之后，青蛙便会在水池中大致分布均匀．
所谓大致分布均匀，就是任取其中一个“格子”，或者它里面有青蛙，或者它的三个邻格里都有青蛙．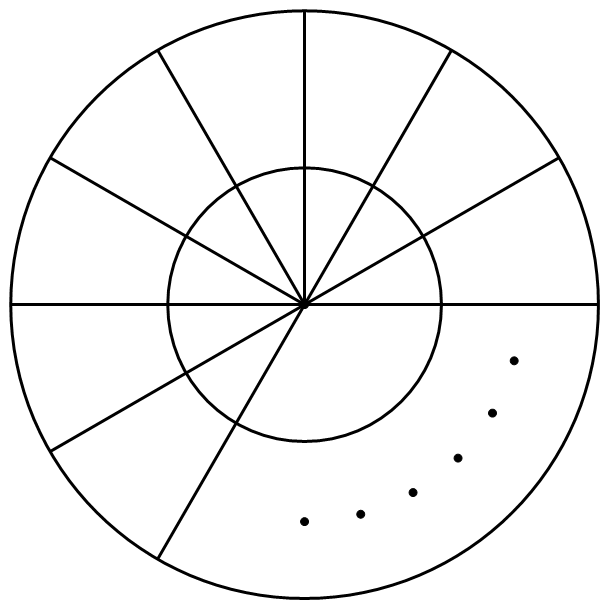
水池中一共跳人了 $4n+ 1$ 只青蛙，青蛙难于安静共处，只 要某个“格子”中有不少于 $3$ 只青蛙，那么迟早一定会有其中 $3$ 只分别同时跳往三个不同邻格．证明：只要经过一段时间之后，青蛙便会在水池中大致分布均匀．
所谓大致分布均匀，就是任取其中一个“格子”，或者它里面有青蛙，或者它的三个邻格里都有青蛙．
【难度】
【出处】
2005第20届CMO试题
【标注】
【答案】
略
【解析】
我们把一个格子中出现一次 $3$ 只青蛙同时分别跳向 三个邻格的事件称为该格子发生一次“爆发＂．而把一个格子或者 是它里面有青蛙，或者是它的三个相邻的格子里面都有青蛙，称为该格子处千“平衡状态"．
容易看出，一个格子只要一旦有青蛙跳入，那么它就一直处于平衡状态””事实上，只要不＂爆发”，那么该格子中的青蛙不会动，它当然处于“平衡状态”；而如果发生”爆发”，那么它的三个邻格中就都有青蛙，并且只要三个邻格都不＂爆发”，那么它就一直 处千“平衡状态”；而不论哪个邻格发生”爆发＂，都会有青蛙跳到 它里面，它里面就一定有青蛙，所以它也一直处于“平衡状态"．
这样一来，为证明题中断言，我们就只要证明：任何一个格子 都迟早会有青蛙跳人．
任取一个格子，把它称为格 $A$，把它所在的扇形称为 $1$ 号扇形，把该扇形中的另一个格子称为格 $B$，如图所示．我们要证明格 $A$ 迟早会有青蛙跳入．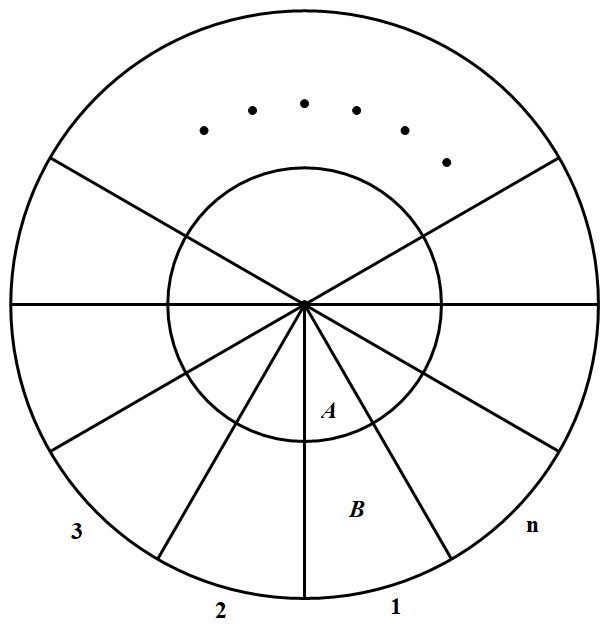
按顺时针方向依次将其余扇形接着编为 $2$ 至 $n$ 号．首先证明 $1$ 号扇形迟早会有青蛙跳人．假设 $1$ 号扇形中永无青蛙到来，那么就不会有青蛙越过 $1$ 号扇形与 $n$ 号扇形之间的隔墙．我们来考察青 蛙所在的扇形编号的平方和．由于没有青蛙进入 $1$ 号扇形（尤其没有青蛙越过 $1$ 号扇形与 $n$ 号扇形之间的隔墙），所以只能是有 $3$ 只青蛙由某个 $k(3\leqslant k \leqslant n - 1)$ 号扇形分别跳人 $k - 1, k$ 和 $k+ 1$ 号扇形各一只，因此平方和的变化量为 $(k-1)^{2}+k^{2}+(k+1)^{2}-3 k^{2}=2$ 即增加 $2$．一方面，由于青蛙的跳动不会停止（因为总有一个格子 里有不少于 $3$ 只青蛙），所以平方和的增加趋势不会停止；但是另 一方面，青蛙所在扇形编号的平方和不可能永无止境地增加下去（不会大于 $(4n+ l)n^2$），由此产生矛盾，所以迟早会有青蛙越过 $1$ 号扇形与 $n$ 号扇形之间的隔墙，进入 $1$ 号扇形．
我们再来证明 $1$ 号扇形迟早会有 $3$ 只青蛙跳人 如果 $1$ 号扇形中至多有两只青蛙跳入，那么它们都不会跳走，并且自始至终上述平方和至多有两次变小（只能在两只青蛙越过 $1$ 号扇形与 $n$ 号扇形之间的隔墙时变小），以后便一直持续不断地上升，从而又重蹈刚才的矛盾 所以 $1$ 号扇形迟早会有 $3$ 只青蛙跳入．
如果这 $3$ 只青蛙中有位于格 $A$ 的，那么格 $A$ 中已经有青蛙跳人；如果这 $3$ 只青蛙全都位于格 $B$，那么格 $B$ 会发生”爆发”，从而有青蛙跳人格 $A$．
容易看出，一个格子只要一旦有青蛙跳入，那么它就一直处于平衡状态””事实上，只要不＂爆发”，那么该格子中的青蛙不会动，它当然处于“平衡状态”；而如果发生”爆发”，那么它的三个邻格中就都有青蛙，并且只要三个邻格都不＂爆发”，那么它就一直 处千“平衡状态”；而不论哪个邻格发生”爆发＂，都会有青蛙跳到 它里面，它里面就一定有青蛙，所以它也一直处于“平衡状态"．
这样一来，为证明题中断言，我们就只要证明：任何一个格子 都迟早会有青蛙跳人．
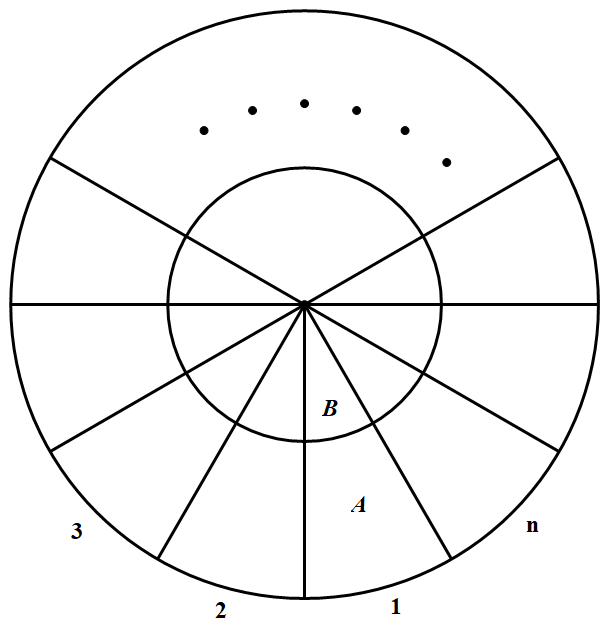
任取一个格子，把它称为格 $A$，把它所在的扇形称为 $1$ 号扇形，把该扇形中的另一个格子称为格 $B$，如图所示．我们要证明格 $A$ 迟早会有青蛙跳入．
按顺时针方向依次将其余扇形接着编为 $2$ 至 $n$ 号．首先证明 $1$ 号扇形迟早会有青蛙跳人．假设 $1$ 号扇形中永无青蛙到来，那么就不会有青蛙越过 $1$ 号扇形与 $n$ 号扇形之间的隔墙．我们来考察青 蛙所在的扇形编号的平方和．由于没有青蛙进入 $1$ 号扇形（尤其没有青蛙越过 $1$ 号扇形与 $n$ 号扇形之间的隔墙），所以只能是有 $3$ 只青蛙由某个 $k(3\leqslant k \leqslant n - 1)$ 号扇形分别跳人 $k - 1, k$ 和 $k+ 1$ 号扇形各一只，因此平方和的变化量为 $(k-1)^{2}+k^{2}+(k+1)^{2}-3 k^{2}=2$ 即增加 $2$．一方面，由于青蛙的跳动不会停止（因为总有一个格子 里有不少于 $3$ 只青蛙），所以平方和的增加趋势不会停止；但是另 一方面，青蛙所在扇形编号的平方和不可能永无止境地增加下去（不会大于 $(4n+ l)n^2$），由此产生矛盾，所以迟早会有青蛙越过 $1$ 号扇形与 $n$ 号扇形之间的隔墙，进入 $1$ 号扇形．我们再来证明 $1$ 号扇形迟早会有 $3$ 只青蛙跳人 如果 $1$ 号扇形中至多有两只青蛙跳入，那么它们都不会跳走，并且自始至终上述平方和至多有两次变小（只能在两只青蛙越过 $1$ 号扇形与 $n$ 号扇形之间的隔墙时变小），以后便一直持续不断地上升，从而又重蹈刚才的矛盾 所以 $1$ 号扇形迟早会有 $3$ 只青蛙跳入．
如果这 $3$ 只青蛙中有位于格 $A$ 的，那么格 $A$ 中已经有青蛙跳人；如果这 $3$ 只青蛙全都位于格 $B$，那么格 $B$ 会发生”爆发”，从而有青蛙跳人格 $A$．
答案
解析
备注
