重置
序号 ID 年级 类型 来源 摘要 创建时间
18826 5c820efe210b284290fc2987 高中 解答题 自招竞赛 在黑板上写有方程
$\left( x-1 \right)\left( x-2 \right)\cdots \left( x-2016 \right)\text{=}\left( x-1 \right)\left( x-2 \right)\cdots \left( x-2016 \right)$
其中等号两边各有 $2016$ 个一次因式．试问：正整数 $k$ 最小为何值时，可以在等号两边擦去这 $4032$ 个一次因式中的恰好 $k$ 个，使得等号每一边都至少留下一个一次因式，且所得到的方程没有实数根？（俄罗斯）		 2022-04-17 19:01:45
18825 5c820f27210b28428f14d310 高中 解答题 自招竞赛 在平面上 $n\geqslant 2$ 条线段，其中任意两条线段都交叉，且没有三条线段相交于同一点．杰夫在每条线段上选取一个端点并放置一只青蛙在此端点上．接着杰夫会拍 $n-1$ 次手．每当他拍一次手时，每只青蛙都立即向前跳到它所在线段上的下一个交点．每只青蛙自始至终不改变跳跃的方向。杰夫的愿望是能够适当地放置青蛙，使得在任何时刻不会有两只青蛙落在同一个交点上．
（a）证明：若 $n$ 是奇数，则杰夫总能实现他的愿望．
（b）证明：若 $n$ 是偶数，则杰夫总不能实现他的愿望．（捷克）		 2022-04-17 19:01:45
18823 5c820e9c210b28428f14d301 高中 解答题 自招竞赛 确定所有正整数 $n$，使得可在一张 $n\times n$ 方格表的每一小方格中填入字母 $I,M,O$ 之一，满足下列条件：
$\bullet $ 在每一行即每一列中，恰有三分之一的小方格填入字母 $I$，三分之一的小方格填入字母 $M$，三分之一的小方格填入字母 $O$；并且
$\bullet $ 在每条对角线上，若该对角线上的小方格个数是三的倍数，则恰有三分之一的小方格填入字母 $I$，三分之一的小方格填入字母 $M$，三分之一的小方格填入字母 $O$．
注：一张 $n\times n$ 方格表的行与列按自然的顺序标记为1至 $n$．由此每个小方格对应一个正整数对 $\left( i\text{,}j \right)$，其中 $1\leqslant i\text{,}j\leqslant n$ 。对 $n\geqslant1$，这张方格表有两类共计 $4n-2$ 条对角线．一条第一类对角线是由 $i+j$ 是某个常数的所有小方格 $\left( i\text{,}j \right)$ 构成，一条第二类对角线是由 $i-j$ 是某个常数的所有小方格 $\left( i\text{,}j \right)$ 构成．（澳大利亚）		 2022-04-17 19:59:44
18817 5c8237de210b28428f14d356 高中 解答题 自招竞赛 设 $n\geqslant 2$ 为一个正整数，考虑由 ${{n}^{2}}$ 个单位正方格构成的 $n\times n$ 的正方形棋盘，一种放置 $n$ 个棋子“车”的方案被称为和平的，如果每一行每一列上正好有一个“车”。求最大的正整数 $k$ 使得对于任何一种和平放置 $n$ 个棋子“车”的方案，都存在一个 $k\times k$ 的棋盘使得它的 ${{k}^{2}}$ 个单位正方格中都没有“车”．（克罗地亚） 2022-04-17 19:54:44
18814 5c823805210b28428f14d360 高中 解答题 自招竞赛 对每一个正整数 $n$，开普敦银行都发行面值为 $\dfrac{1}{n}$ 的硬币．给定总额不超过 $99+\dfrac{1}{2}$ 的有限多个这样的硬币（面值不必两两不同），证明可以把它们分为至多 $100$ 组，使得每一组中硬币的面值之和最多是 $1$．（卢森堡） 2022-04-17 19:52:44
18813 5c82380c210b28428f14d365 高中 解答题 自招竞赛 平面上的一族直线被称为是处于一般位置的，如果其中没有两条直线平行，没有三条直线共点．一族处于一般位置的直线把平面分割成若干区域，我们把其中面积有限的区域称为这族直线的有限区域．证明：对于充分大的 $n$ 和任意处于一般位置的 $n$ 条直线，我们都可以把其中至少 $\sqrt{n}$ 条直线染成蓝色，使得每一个有限区域的边界都不全是蓝色的．
注：如果你的答卷上证明的是 $c\sqrt{n}$（而不是 $\sqrt{n}$）的情形，那么将会根据常数 $c$ 的值给分．（奥地利）		 2022-04-17 19:51:44
18810 5c85c055210b28428f14d374 高中 解答题 自招竞赛 平面上的 $4027$ 个点称为是一个哥伦比亚式点集，如果其中任意三点不共线，且有 $2013$ 个点是红色的，$2014$ 个点是蓝色的．在平面上画出一组直线，可以将平面分成若干区域．如果一组直线对于一个哥伦比亚式点集满足下述两个条件，我们就称这是一个好直线组：
（1）这些直线不经过该哥伦比亚式点集中的任何一个点；
（2）每个区域中都不会同时出现两种颜色的点．
求 $k$ 的最小值，使得对于任意的哥伦比亚式点集，都存在由 $k$ 条直线构成的好直线组．（澳大利亚）		 2022-04-17 19:50:44
18806 5c85c084210b284290fc29f5 高中 解答题 自招竞赛 设整数 $n\geqslant 3$，在圆周上有 $n+1$ 个等分点．用数 $0,1,\ldots,n$ 标记这些点，每个数字恰好用一次．考虑所有可能的标记方式：如果一种标记方式可以由另一种标记方式通过圆的旋转得到，那么认为这两种标记方式是同一个．一种标记方式称为是漂亮的，如果对于任意满足 $a+d=b+c$ 的四个标记数 $a<b<c<d$，连接标 $a$ 和 $d$ 的点的弦与连接标 $b$ 和 $c$ 的点的弦都不相交．
设 $M$ 是漂亮的标记方式的总数，又设 $N$ 是满足 $x+y\leqslant n$，且 $\text{gcd}(x,y)=1$ 的有序正整数对 $(x,y)$ 的个数．
证明：$M=N+1$．（俄罗斯）		 2022-04-17 19:47:44
18803 5c85c441210b28428f14d38b 高中 解答题 自招竞赛 “欺诈猜数游戏”在两个玩家甲和乙之间进行，游戏依赖于两个甲和乙都知道的正整数 $k$ 和 $n$．
游戏开始时甲先选定两个整数 $x$ 和 $N$，$1\leqslant x\leqslant N$．甲如实告诉乙 $N$ 的值，但对 $x$ 守口如瓶．乙现在试图通过如下方式的提问来获得关于 $x$ 的信息：每次提问，乙任选一个由若干正整数组成的集合 $S$（可以重复使用之前提问中使用过的集合），问甲“$x$ 是否属于 $S$？”乙可以提任意数量的题．在乙每次提问之后，甲必须对乙的提问立刻回答“是”或“否”，甲可以说谎话，并且说谎的次数没有限制，唯一的限制是甲在任意连续 $k +1$ 次回答中至少有一次回答是真话．
在乙问完所有想问的问题之后，乙必须指出一个至多包含 $n$ 个正整数的集合 $X$，若 $x$ 属于 $X$，则乙获胜；否则甲获胜．证明：
（1）若 $n\geqslant 2^k$，则乙可保证获胜；
（2）对所有充分大的整数 $k$，存在整数 $n\geqslant 1.99^k$，使得乙无法保证获胜．（加拿大）		 2022-04-17 19:45:44
18795 5c85c8cd210b284290fc2a16 高中 解答题 自招竞赛 对任意由 $4$ 个不同正整数组成的集合 $A=\{a_{1},a_{2},a_{3},a_{4}\}$，记 $s_{A}=a_{1}+a_{2}+a_{3}+a_{4}$，设 $n_{A}$ 是满足 $a_{i}+a_{j}~(1\leqslant i<j\leqslant 4)$ 整除 $s_{A}$ 的数对 $(i,j)$ 的个数．求所有由 $4$ 个不同正整数组成的集合 $A$，使得达到最大值．（墨西哥） 2022-04-17 19:41:44
18786 5c85c8da210b28428f14d3a8 高中 解答题 自招竞赛 设 $S$ 是平面上包含至少两个点的一个有限点集，其中没有三点在同一条直线上．
所谓一个“风车”是指这样一个过程：从经过 $S$ 中单独一点 $P$ 的一条直线 $\ell$ 开始，以 $P$ 为旋转中心顺时针旋转，直至首次遇到 $S$ 中的另一点，记为点 $Q$．接着这条直线以 $Q$ 为新的旋转中心顺时针旋转，直到再次遇到 $S$ 中的某一点，这样的过程无限持续下去．
证明：可以适当选取 $S$ 中的一点 $P$，以及过 $P$ 的一条直线 $\ell$，使得由此产生的“风车”将 $S$ 中的每一点都无限多次用作旋转中心．（英国）		 2022-04-17 19:35:44
18784 5c85c8eb210b28428f14d3ad 高中 解答题 自招竞赛 给定整数 $n>0$．有一个天平和 $n$ 个重量分别为 $2^{0},2^{1},\ldots,2^{n-1}$ 的砝码．
现通过 $n$ 步操作逐个将所有砝码都放上天平，使得在操作过程中，右边的重量总不超过左边的重量．每一步操作是从尚未放上天平的砝码中选择一个砝码，将其放到天平的左边或右边，直至所有砝码都被放上天平．
求整个操作过程的不同方法个数．（伊朗）		 2022-04-17 19:35:44
18764 5c85cdc8210b284290fc2a34 高中 解答题 自招竞赛 有 $6$ 个盒子 $B_{1},B_{2},B_{3},B_{4},B_{5},B_{6}$，开始时每个盒子中都恰好有一枚硬币．每次可以任意选择如下两种方式之一对它们进行操作：
方式1：选取一个至少有一枚硬币的盒子 $B_{j}~(1\leqslant j\leqslant 5)$，从盒子 $B_{j}$ 中取走一枚硬币，并在盒子 $B_{j+1}$ 中加入 $2$ 枚硬币．
方式2：选取一个至少有一枚硬币的盒子 $B_{k}~(1\leqslant k\leqslant 4)$，从盒子 $B_{k}$ 中取走一枚硬币，并且交换盒子 $B_{k+1}$（可能是空盒）与盒子 $B_{k+2}$（可能是空盒）中的所有硬币．
问：是否可以进行若干次上述操作，使得盒子 $B_{1},B_{2},B_{3},B_{4},B_{5}$ 中没有硬币，而盒子 $B_{6}$ 中恰好有 $2010^{2010^{2010}}$ 枚硬币？（注：$a^{b^{c}}=a^{(b^{c})}$．）（荷兰）		 2022-04-17 19:24:44
18726 5c85d34e210b284290fc2a61 高中 解答题 自招竞赛 设 $a_{1},a_{2},\ldots,a_{n}$ 是互不相同的正整数．$M$ 是有 $n-1$ 个元素的正整数集，且不含数 $s=a_{1}+a_{2}+\ldots+a_{n}$．一只蚱蜢沿着实数轴从原点 $0$ 开始向右跳跃 $n$ 步，它的跳跃距离是 $a_{1},a_{2},\ldots,a_{n}$ 的某个排列．证明：可以选择一种排列，使得蚱蜢跳跃落下的点所表示的数都不在集 $M$ 中．（俄罗斯） 2022-04-17 19:04:44
18720 5c85d6f2210b284290fc2a6b 高中 解答题 自招竞赛 设 $n$ 和 $k$ 是正整数，$k\geqslant n$，且 $k-n$ 是一个偶数．$2n$ 盏灯依次编号为 $1,2,\ldots,2n$，每一盏灯可以“开”和“关”．开始时，所有的灯都是“关”的．对这些灯可进行操作，每一次操作只改变其中的一盏灯的开关状态（即“开”变成“关”，“关”变成“开”），我们考虑长度为 $k$ 的操作序列，序列中的第 $i$ 项就是第 $i$ 次操作时被改变开关状态的那盏灯的编号．
设 $N$ 是 $k$ 次操作后使得灯 $1,\ldots,n$ 是“开”的，灯 $n+1,\ldots,2n$ 是“关”的状态的所有不同的操作序列的个数．
设 $M$ 是 $k$ 次操作后使得灯 $1,\ldots,n$ 是“开”的，灯 $n+1,\ldots,2n$ 是“关”的，但是灯 $n+1,\ldots,2n$ 始终没有被开过的所有不同的操作序列的个数．
求比值 $\dfrac{N}{M}$．（法国）		 2022-04-17 19:01:44
18714 5c85dade210b28428f14d432 高中 解答题 自招竞赛 在一次数学竞赛活动中，有一些参赛选手是朋友．朋友关系是相互的，如果一群参赛选手中的任何两人都是朋友，我们就称这一群选手为一个“团”（特别地，人数少于2的一群也是一个团）．
已知在这次竞赛中，最大的团（人数最多的团）的人数是一个偶数，证明：我们总能把参赛选手分配到两个教室，使得一个教室的最大团的人数等于另一个教室中的最大团的人数．（俄罗斯）		 2022-04-17 19:57:43
18711 5c85daf5210b28428f14d43f 高中 解答题 自招竞赛 设 $n$ 是一个正整数．考虑 $S=\{(x,y,z):~x,y,z\in\{0,1,\ldots,n\},x+y+z>0\}$ 这样一个三维空间中具有 $(n+1)^{3}-1$ 个点的集合，问：最少要多少个平面，它们的并集才能包含 $S$，但不包含 $(0,0,0)$．（荷兰） 2022-04-17 19:56:43
18709 5c85de84210b28428f14d44c 高中 解答题 自招竞赛 设 $P$ 为正 $2006$ 边形．如果 $P$ 的一条对角线的两端将 $P$ 的边界分成两部分，每部分都包含 $P$ 的奇数条边，那么该对角线称为“好边”．规定 $P$ 的每条边均为“好边”．已知 $2003$ 条在 $P$ 内部不相交的对角线将 $P$ 分割成若干三角形．试问在这种分割之下，最多有多少个有两条“好边”的等腰三角形？（塞尔维亚） 2022-04-17 19:55:43
18698 5c85ed93210b28428f14d475 高中 解答题 自招竞赛 某次数学竞赛共有 $6$ 个试题，其中任意两个试题都被超过 $\dfrac{2}{5}$ 的参赛者答对了．但没有一个参赛者能答对所有的 $6$ 个试题．证明：至少有两个参赛者都恰好答对了 $5$ 个试题．（罗马尼亚） 2022-04-17 19:48:43
18672 5c85f2c3210b28428f14d487 高中 解答题 自招竞赛 由 $6$ 个单位正方形构成如下图形以及它的旋转或翻转所得到的图形统称为钩形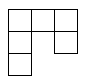．试确定所有 $m×n$ 的矩形，使其能被钩形所覆盖，要求：
（1）覆盖矩形时，不能有空隙，钩形之间不重叠；
（2）钩形不能覆盖到矩形外．（爱沙尼亚）		 2022-04-17 19:33:43
0.185900s