设整数 $n\geqslant 3$,在圆周上有 $n+1$ 个等分点.用数 $0,1,\ldots,n$ 标记这些点,每个数字恰好用一次.考虑所有可能的标记方式:如果一种标记方式可以由另一种标记方式通过圆的旋转得到,那么认为这两种标记方式是同一个.一种标记方式称为是漂亮的,如果对于任意满足 $a+d=b+c$ 的四个标记数 $a<b<c<d$,连接标 $a$ 和 $d$ 的点的弦与连接标 $b$ 和 $c$ 的点的弦都不相交.
设 $M$ 是漂亮的标记方式的总数,又设 $N$ 是满足 $x+y\leqslant n$,且 $\text{gcd}(x,y)=1$ 的有序正整数对 $(x,y)$ 的个数.
证明:$M=N+1$.(俄罗斯)
设 $M$ 是漂亮的标记方式的总数,又设 $N$ 是满足 $x+y\leqslant n$,且 $\text{gcd}(x,y)=1$ 的有序正整数对 $(x,y)$ 的个数.
证明:$M=N+1$.(俄罗斯)
【难度】
【出处】
2013年第54届IMO试题
【标注】
【答案】
略
【解析】
证法一
我们要注意到,题目的条件决定了圆周上的标记点的间距是无关紧要的,决定相关的弦是否相交的,仅仅是各点之间的次序关系.对于 $[0,n]=\{0,1,\ldots,n\}$ 的一个循环排列,我们定义一条 $k$ -弦为一条(可能退化的)弦,其(可能重合的)两个端点(上的数)之和为 $k$.我们称圆的三条弦是顺次的,如果其中的一条弦的两侧各有一条弦.我们称 $m\geqslant 3$ 条弦是顺次的,如果其中任意三条弦是顺次的.例如在图中 $A,B$ 和 $C$ 是顺次的,但是 $B,C$ 和 $D$ 则不是顺次的.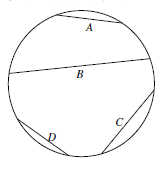 辅助命题:在一个漂亮排列中,对于任意的整数 $k$,$k$ -弦全体是顺次的.
辅助命题:在一个漂亮排列中,对于任意的整数 $k$,$k$ -弦全体是顺次的.
命题的证明:我们用数学归纳法.对于 $k\leqslant 3$,命题是平凡的.现在设 $n\geqslant 4$,用反证法.假设有一个漂亮排列 $S$,使得三条 $k$ -弦 $A,B$ 和 $C$ 不是顺次的.如果数 $n$ 不是 $A,B,C$ 的端点,那么我们可以在 $S$ 中去掉 $n$ 这个点,得到 $[0,n-1]$ 的一个漂亮排列 $S\backslash\{n\}$,那样由归纳假设就可以知道 $A,B$ 和 $C$ 是顺次的.同理,如果 $0$ 不是 $A,B,C$ 的端点,那么去掉 $0$,再把其他所有的数都减去 $1$,就可以得到一个漂亮排列 $S\backslash \{0\}$,这样 $A,B$ 和 $C$ 就是顺次的.因此 $0$ 和 $n$ 必然都出现在这三条弦的端点中.假设 $0$ 所在的弦的另一端点是 $x$,$n$ 所在的弦的另一端点是 $y$,那么 $n\geqslant 0+x=k=n+y\geqslant n$.所以 $0$ 和 $n$ 是同一条弦的端点,不妨设为 $C$.
设 $D$ 是以圆周上分别和 $0,n$ 相邻,且相对于 $C$ 和 $A,B$ 同侧的数 $u$ 和 $v$ 为端点的弦,如图所示. 记 $t=u+v$.如果我们有 $t=n$,那么 $A,B$ 和 $D$ 在漂亮排列 $S\backslash \{0,n\}$ 中就不是顺次的,和归纳假设矛盾.如果 $t<n$,那么从 $0$ 到 $t$ 的 $t$ -弦不能和 $D$ 相交,这样弦 $C$ 就把 $t$ 和弦 $D$ 分隔开了.而 $t$ 到 $n-t$ 的弦与 $C$ 不相交,这样 $t$ 和 $n-t$ 就位于 $C$ 的同侧.但是这样在 $S\backslash \{0,n\}$ 中,$A,B$ 和 $E$ 就不是顺次的,矛盾.最后,因为 $x\mapsto n-x$($0\leqslant x\leqslant n$)保持一个循环排列的漂亮性(只是把 $t$ -弦都映到了 $(2n-t)$ -弦),所以 $t>n$ 和 $t<n$ 是等价的.这样就证明了辅助命题.
记 $t=u+v$.如果我们有 $t=n$,那么 $A,B$ 和 $D$ 在漂亮排列 $S\backslash \{0,n\}$ 中就不是顺次的,和归纳假设矛盾.如果 $t<n$,那么从 $0$ 到 $t$ 的 $t$ -弦不能和 $D$ 相交,这样弦 $C$ 就把 $t$ 和弦 $D$ 分隔开了.而 $t$ 到 $n-t$ 的弦与 $C$ 不相交,这样 $t$ 和 $n-t$ 就位于 $C$ 的同侧.但是这样在 $S\backslash \{0,n\}$ 中,$A,B$ 和 $E$ 就不是顺次的,矛盾.最后,因为 $x\mapsto n-x$($0\leqslant x\leqslant n$)保持一个循环排列的漂亮性(只是把 $t$ -弦都映到了 $(2n-t)$ -弦),所以 $t>n$ 和 $t<n$ 是等价的.这样就证明了辅助命题.
下面我们用归纳法证明原命题.$n=2$ 的情形是平凡的.现在假设 $n\geqslant 3$.设 $S$ 是 $[0,n]$ 的一个漂亮排列,把 $n$ 去掉以后得到的 $[0,n-1]$ 的循环排列记为 $T$.在 $T$ 中,全体 $n$ -弦是顺次的,
且这些弦的端点包括除了 $0$ 以外的所有数.这样我们称 $T$ 是第一型的,如果 $0$ 位于两条 $n$ -弦之间,否则称 $T$ 为第二型的.我们将证明,
$[0,n-1]$ 的每个第一型漂亮排列恰对应于一个 $[0,n]$ 的漂亮排列,而 $[0,n-1]$ 的每个第二型漂亮排列恰对应于两个 $[0,n]$ 的漂亮排列.
如果 $T$ 是第一型的,设 $0$ 在弦 $A$ 和弦 $B$ 之间.因为在 $S$ 中从 $0$ 到 $n$ 的弦和 $A,B$ 是顺次的,所以 $n$ 必然位于 $A,B$ 之间的另一端弧上.这样从 $T$ 出发有为唯一的方式复原 $S$.另一方面,从每个第一型的 $T$ 出发,按照上述方式加上 $n$,我们来说明得到的循环排列 $S$ 一定是漂亮的.对于 $0<k<n$,$S$ 的 $k$ -弦必然也是 $T$ 的 $k$ -弦,所以他们是顺次的.而对于 $n<k<2n$,注意到 $S$ 的 $n$ -弦是互相平行的,所以存在一根轴 $l$,使得对于任意的 $x$,$x$ 和 $n-x$ 关于 $l$ 是对称的.如果有两条 $k$ -弦是相交的,那么它们关于 $l$ 的对称像是两条 $(2n-k)$ -弦,也是相交的.但是此时 $0<2n-k<n$,矛盾.
如果 $T$ 是第二型的,那么在对应的 $S$ 中 $n$ 的位置有两种可能,即在 $0$ 的两侧与之相邻.同上可以验证这样得到的都是 $[0,n]$ 的漂亮排列.
这样如果我们记 $[0,n]$ 的漂亮排列总数为 $M_n$,以 $L_n$ 记 $[0,n-1]$ 的第二型漂亮排列的总数,我们就有
$\begin{aligned} M_{n} &=\left(M_{n-1}-L_{n-1}\right)+2 L_{n-1} \\ &=M_{n-1}+L_{n-1} \end{aligned}$
下面只要说明 $L_{n-1}$ 等于满足 $x+y=n$,且 $\text{gcd}(x,y)=1$ 的正整数对 $(x,y)$ 的个数.因为 $n\geqslant 3$,所以这个数等于
$
\varphi(n)=\{x, 1 \leqslant x \leqslant n, \operatorname{gcd}(x, n)=1\}
$
为了证明这一点,考虑 $[0,n-1]$ 的一个第二型漂亮排列.沿顺时针方向在圆周上标记位置 $0,\ldots,n-1\pmod{n}$,使得数 $0$ 位于位置 $0$.记位置 $i$ 上的数为 $f(i)$;注意 $f$ 是 $[0,n-1]$ 的一个置换.设位置 $a$ 上的数是 $n-1$,即 $f(a)=n-1$.
因为除了 $0$ 以外所有的数都在一个 $n$ -弦中,且 $n$ -弦全体是顺次的,并且 $0$ 两侧的两个位置的连线是一条 $n$ -弦,所以所有的 $n$ -弦是平行的
(此时假设各点间距相同),即对于任意的 $i$,我们有
$f(i)+f(-i)=n$
类似地,因为 $(n-1)$ -弦全体是顺次的,且每个点都属于一条 $(n-1)$ -弦,
所以这些弦互相都是平行的,且对于任意的 $i$,有
$f(i)+f(a-i)=n-1$
所以对于任意的 $i$,$f(a-i)=f(-i)-1$;而由于 $f(0)=0$,我们得到对于任意的 $k$,
$f(-a k)=k$ ①
上面这个等式是模 $n$ 意义下的.因为 $f$ 是一个置换,我们必有 $(a,n)=1$,即
$
L_{n-1} \leqslant \varphi(n)
$
为证明等号成立.只需注意到 ① 给出的是一个漂亮排列.为此我们考虑圆周上满足 $w+y=x+z$ 的四个数 $w,x,y,z$.它们在圆周上的位置满足
$(-aw)+(-ay)=(-ax)+(-az)$.
即连结 $w$ 和 $y$ 的弦与连结 $x$ 和 $z$ 的弦是平行的.这样 ① 是漂亮的,且由构造可知这是第二型的.即得证明.
证法二
我们要注意到,题目的条件决定了圆周上的标记点的间距是无关紧要的,决定相关的弦是否相交的,仅仅是各点之间的次序关系.注意到 $(0,1)$ 中恰有 $N$ 个分母不超过 $n$ 的既约分数 $f_1 <\ldots< f_N$,因为每个满足 $x+y\leqslant n$,且 $\text{gcd}(x,y)=1$ 的正整数对 $(x,y)$ 都对应到分数 $\dfrac{x}{(x+y)}$.对于 $1\leqslant i\leqslant N$,记 $f_i = \dfrac{a_i}{b_i}$.
我们首先来构造 $N+1$ 个漂亮排列.考虑不等于上述 $N$ 个分数的任意一个 $\alpha\in(0,1)$.取一个周长为 $1$ 的圆周.我们顺次在圆上标记点 $0,1,2,\ldots,n$.其中 $0$ 点的位置是任意的,而从 $i$ 到 $i+1$ 我们沿顺时针方向前进 $\alpha$.这样标记 $k$ 的点到标记 $0$ 的点的顺时针方向的距离就是 $\{k\alpha\}$,其中 $\{r\}$ 表示 $r$ 的小数部分.称这样的一个漂亮排列是循环的,记为 $A(\alpha)$.如果 $A(\alpha_1)$ 和 $A(\alpha_2)$ 的各标记点的顺时针次序是相同的,
我们就认为它们是同一个标记方式.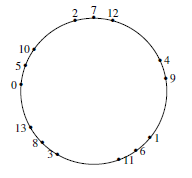 图是 $[1,13]$ 对于某个充分小的 $\varepsilon >0$ 的 $A(\dfrac{3}{5}+\varepsilon)$.
图是 $[1,13]$ 对于某个充分小的 $\varepsilon >0$ 的 $A(\dfrac{3}{5}+\varepsilon)$.
如果 $a<b<c<d$ 满足 $a+d=b+c$,那么 $a\alpha+d\alpha=b\alpha+c\alpha$,所以在 $A(\alpha)$ 中连接标记 $a$ 和 $d$ 的点的弦与连结标记 $b$ 和 $c$ 的点的弦是平行的.这样在每个循环排列中,对于任意的 $k$,所有 $k$ -弦都是相互平行的.从而每一个循环排列都是漂亮的.
下面我们来说明恰好有 $N+1$ 种不同的循环排列.为此考察当 $\alpha$ 从 $0$ 递增到 $1$ 时 $A(\alpha)$ 的变化方式.标记 $p$ 的点和标记 $q$ 时点的位置顺序发生改变当且仅当 $\alpha$ 满足 $\{p\alpha\}=\{q\alpha\}$;而这种情况只会在 $\alpha$ 等于前述 $N$ 个分数之一的时候发生.这样最多就只能有 $N+1$ 种不同的循环排列.
要证明这些循环排列的确是两两不同的.对于充分小的 $\varepsilon>0$,和某个 $f_i=\frac{a_i}{b_i}$,考虑 $A(f_i +\varepsilon)$.那么标记为 $k$ 的点的(顺时针)位置在 $\frac{ka_{i}\pmod{b_i}}{b_i}+k\varepsilon$.这样所有的点可以根据这个位置表达式的第一项的值分成 $b_i$ 组.介于 $\frac{k}{b_i}$ 和 $\frac{k+1\pmod{b_i}}{b_i}$ 之间的点所标记的数对应的是 $ka_{i}^{-1}\pmod{b_i}$ 在 $0$ 到 $n$ 之间的不同取值(且按照从小到大依次排列).这样在 $A(f_i +\varepsilon)$ 中,
从 $0$ 出发,顺时针方向的第一个标记数是 $b_i$,而从 $0$ 出发往顺时针方向碰到的第一个比 $b_i$ 小的数是 $a_{i}^{-1}\pmod{b_i}$,而由这个数可以唯一地确定 $a_i$.这样从一个循环排列出发我们可以唯一地确定 $f_i$.同时注意到上述定义的循环排列 $A(f_i + \varepsilon)$ 是不包括顺时针方向顺次写上 $0,1,2,\ldots,n$ 这样一个"平凡"排列的,所以我们可以知道 $N+1$ 个循环排列 $A(\varepsilon),A(f_1 +\varepsilon),\ldots,A(f_N +\varepsilon)$ 是两两不同的.
下面我们观察到一个有用的事实:
如果 $f_i < \alpha < f_{i+1}$,那么在 $A(\alpha)$ 中从 $0$ 出发,顺时针方向第一个数是 $b_i$,逆时针方向第一个数是 $b_{i+1}$.②
事实上,我们已经对 $A(\alpha)=A(f_i +\varepsilon)$ 证明了前半部分,用同样的理由可以对 $A(\alpha)=A(f_{i+1}-\varepsilon)$ 证明后半部分.
最后,我们通过用对于 $n$ 的归纳来证明 $[0,n]$ 的所有漂亮标记都是循环排列.对于 $n=3$,这是显然的.现在假设 $[0,n-1]$ 的所有漂亮标记方法都是循环排列.我们考虑 $[0,n]$ 的一个漂亮标记方法 $A$.这样 $A_{n-1}=A\{n\}$ 是 $[0,n-1]$ 的一个漂亮标记方法,从而是一个循环排列.设 $A_{n-1}=A_{n-1}(\alpha)$.
假设在 $n-1$ 阶Farey序列(即分母不超过 $n-1$ 的 $(0,1)$ 之间的分数从小到大排列)中,$\alpha$ 介于相邻的两个分数 $\frac{p_1}{q_1}<\frac{p_2}{q_2}$ 之间,因为对于 $0<i\leqslant n-1$,
都成立 $\frac{i}{n}<\frac{i}{n-1}\leqslant\frac{i+1}{n}$,
所以在 $n$ 阶Farey序列中,至多有一个分母为 $n$ 的分数夹在这两个分数之间.
情形一:$\frac{p_1}{q_1}$ 和 $\frac{p_2}{q_2}$ 之间没有分母为 $n$ 的分数.
首先设在 $A_n (\alpha)$ 中,$n$ 介于 $x$ 和 $y$ 之间(顺时针方向依次为 $x,n,y$).由前述事实 ②,我们知道 $0$ 两边的数分别是 $q_1$ 和 $q_2$.
所以 $x,y\geqslant 1$.
由前述讨论可以知道,$x=n-b_i$ 关于某个 $k$ 满足 $x\equiv ka_{i}^{-1}\pmod{b_i}$,而 $y$ 则是 $y\equiv (k+1)a_{i}^{-1}\pmod{b_i}$ 在 $[1,n]$ 中的最小解.
同理,$x-1=(n-1)-b_i$ 关于某个 $k'$ 满足 $x-1\equiv k'a_{i}^{-1}\pmod{b_i}$,这样 $y-1\equiv (k'+1)a_{i}^{-1}\pmod{b_i}$,而且是 $[0,n]$ 满足上述同余方程的数中最小的一个.
所以在 $A_n (\alpha)$ 中,$x,y,x-1,n-1,y-1$ 顺时针方向顺次出现
(可能出现 $x=y-1$ 或者 $y=x-1$ 的情况).
现在我们注意到 $A$ 和 $A_n (\alpha)$ 相比最多只有 $n$ 的位置可能不同.
在 $A$ 中,因为连结 $x$ 和 $n-1$ 的弦与连结 $x-1$ 和 $n$ 的弦不相交,所以(沿顺时针方向)$n$ 就一定在 $x$ 和 $n-1$ 之间.同理(沿顺时针方向)$n$ 也一定在 $n-1$ 和 $y$ 之间.这样(沿顺时针方向)$n$ 就必定在 $x$ 和 $y$ 之间,从而 $A$ 就是一个循环排列.
情形二:$\frac{p_1}{q_1}$ 和 $\frac{p_2}{q_2}$ 之间恰有一个分母为 $n$ 的分数.
此时有两个循环排列 $A_n (\alpha_1)$ 和 $A_n (\alpha_2)$,去掉 $n$ 以后都得到 $A_{n-1}(\alpha)$,分别对应与 $\frac{p_1}{q_1}<\alpha_1<\frac{i}{n}$ 和 $\frac{i}{n}<\alpha_2<\frac{p_2}{q_2}$.
在 $A_{n-1}(\alpha)$ 中,由前述事实 ② 可知顺时针方向连续顺次出现 $q_2 , 0 , q_1$.同理,在 $A_n (\alpha_1)$ 中,顺时针方向连续顺次出现 $q_2 , n , 0 ,q_1$;在 $A_n (\alpha_2)$ 中,顺时针方向连续顺次出现 $q_2 , 0 , n , q_1$. 令 $x=q_2 , y=q_1$ 和情形1同样讨论可知在 $A$ 中,$n$ 也必然位于 $x$ 和 $y$ 之间,这样 $A$ 要么等价于 $A_n (\alpha_1)$,要么等价于 $A_n (\alpha_2)$.
令 $x=q_2 , y=q_1$ 和情形1同样讨论可知在 $A$ 中,$n$ 也必然位于 $x$ 和 $y$ 之间,这样 $A$ 要么等价于 $A_n (\alpha_1)$,要么等价于 $A_n (\alpha_2)$.
综上所述,每一个漂亮的标记法都是一个循环排列.由此命题得证.
我们要注意到,题目的条件决定了圆周上的标记点的间距是无关紧要的,决定相关的弦是否相交的,仅仅是各点之间的次序关系.对于 $[0,n]=\{0,1,\ldots,n\}$ 的一个循环排列,我们定义一条 $k$ -弦为一条(可能退化的)弦,其(可能重合的)两个端点(上的数)之和为 $k$.我们称圆的三条弦是顺次的,如果其中的一条弦的两侧各有一条弦.我们称 $m\geqslant 3$ 条弦是顺次的,如果其中任意三条弦是顺次的.例如在图中 $A,B$ 和 $C$ 是顺次的,但是 $B,C$ 和 $D$ 则不是顺次的.
 辅助命题:在一个漂亮排列中,对于任意的整数 $k$,$k$ -弦全体是顺次的.
辅助命题:在一个漂亮排列中,对于任意的整数 $k$,$k$ -弦全体是顺次的.命题的证明:我们用数学归纳法.对于 $k\leqslant 3$,命题是平凡的.现在设 $n\geqslant 4$,用反证法.假设有一个漂亮排列 $S$,使得三条 $k$ -弦 $A,B$ 和 $C$ 不是顺次的.如果数 $n$ 不是 $A,B,C$ 的端点,那么我们可以在 $S$ 中去掉 $n$ 这个点,得到 $[0,n-1]$ 的一个漂亮排列 $S\backslash\{n\}$,那样由归纳假设就可以知道 $A,B$ 和 $C$ 是顺次的.同理,如果 $0$ 不是 $A,B,C$ 的端点,那么去掉 $0$,再把其他所有的数都减去 $1$,就可以得到一个漂亮排列 $S\backslash \{0\}$,这样 $A,B$ 和 $C$ 就是顺次的.因此 $0$ 和 $n$ 必然都出现在这三条弦的端点中.假设 $0$ 所在的弦的另一端点是 $x$,$n$ 所在的弦的另一端点是 $y$,那么 $n\geqslant 0+x=k=n+y\geqslant n$.所以 $0$ 和 $n$ 是同一条弦的端点,不妨设为 $C$.
设 $D$ 是以圆周上分别和 $0,n$ 相邻,且相对于 $C$ 和 $A,B$ 同侧的数 $u$ 和 $v$ 为端点的弦,如图所示.
 记 $t=u+v$.如果我们有 $t=n$,那么 $A,B$ 和 $D$ 在漂亮排列 $S\backslash \{0,n\}$ 中就不是顺次的,和归纳假设矛盾.如果 $t<n$,那么从 $0$ 到 $t$ 的 $t$ -弦不能和 $D$ 相交,这样弦 $C$ 就把 $t$ 和弦 $D$ 分隔开了.而 $t$ 到 $n-t$ 的弦与 $C$ 不相交,这样 $t$ 和 $n-t$ 就位于 $C$ 的同侧.但是这样在 $S\backslash \{0,n\}$ 中,$A,B$ 和 $E$ 就不是顺次的,矛盾.最后,因为 $x\mapsto n-x$($0\leqslant x\leqslant n$)保持一个循环排列的漂亮性(只是把 $t$ -弦都映到了 $(2n-t)$ -弦),所以 $t>n$ 和 $t<n$ 是等价的.这样就证明了辅助命题.
记 $t=u+v$.如果我们有 $t=n$,那么 $A,B$ 和 $D$ 在漂亮排列 $S\backslash \{0,n\}$ 中就不是顺次的,和归纳假设矛盾.如果 $t<n$,那么从 $0$ 到 $t$ 的 $t$ -弦不能和 $D$ 相交,这样弦 $C$ 就把 $t$ 和弦 $D$ 分隔开了.而 $t$ 到 $n-t$ 的弦与 $C$ 不相交,这样 $t$ 和 $n-t$ 就位于 $C$ 的同侧.但是这样在 $S\backslash \{0,n\}$ 中,$A,B$ 和 $E$ 就不是顺次的,矛盾.最后,因为 $x\mapsto n-x$($0\leqslant x\leqslant n$)保持一个循环排列的漂亮性(只是把 $t$ -弦都映到了 $(2n-t)$ -弦),所以 $t>n$ 和 $t<n$ 是等价的.这样就证明了辅助命题.下面我们用归纳法证明原命题.$n=2$ 的情形是平凡的.现在假设 $n\geqslant 3$.设 $S$ 是 $[0,n]$ 的一个漂亮排列,把 $n$ 去掉以后得到的 $[0,n-1]$ 的循环排列记为 $T$.在 $T$ 中,全体 $n$ -弦是顺次的,
且这些弦的端点包括除了 $0$ 以外的所有数.这样我们称 $T$ 是第一型的,如果 $0$ 位于两条 $n$ -弦之间,否则称 $T$ 为第二型的.我们将证明,
$[0,n-1]$ 的每个第一型漂亮排列恰对应于一个 $[0,n]$ 的漂亮排列,而 $[0,n-1]$ 的每个第二型漂亮排列恰对应于两个 $[0,n]$ 的漂亮排列.
如果 $T$ 是第一型的,设 $0$ 在弦 $A$ 和弦 $B$ 之间.因为在 $S$ 中从 $0$ 到 $n$ 的弦和 $A,B$ 是顺次的,所以 $n$ 必然位于 $A,B$ 之间的另一端弧上.这样从 $T$ 出发有为唯一的方式复原 $S$.另一方面,从每个第一型的 $T$ 出发,按照上述方式加上 $n$,我们来说明得到的循环排列 $S$ 一定是漂亮的.对于 $0<k<n$,$S$ 的 $k$ -弦必然也是 $T$ 的 $k$ -弦,所以他们是顺次的.而对于 $n<k<2n$,注意到 $S$ 的 $n$ -弦是互相平行的,所以存在一根轴 $l$,使得对于任意的 $x$,$x$ 和 $n-x$ 关于 $l$ 是对称的.如果有两条 $k$ -弦是相交的,那么它们关于 $l$ 的对称像是两条 $(2n-k)$ -弦,也是相交的.但是此时 $0<2n-k<n$,矛盾.
如果 $T$ 是第二型的,那么在对应的 $S$ 中 $n$ 的位置有两种可能,即在 $0$ 的两侧与之相邻.同上可以验证这样得到的都是 $[0,n]$ 的漂亮排列.
这样如果我们记 $[0,n]$ 的漂亮排列总数为 $M_n$,以 $L_n$ 记 $[0,n-1]$ 的第二型漂亮排列的总数,我们就有
$\begin{aligned} M_{n} &=\left(M_{n-1}-L_{n-1}\right)+2 L_{n-1} \\ &=M_{n-1}+L_{n-1} \end{aligned}$
下面只要说明 $L_{n-1}$ 等于满足 $x+y=n$,且 $\text{gcd}(x,y)=1$ 的正整数对 $(x,y)$ 的个数.因为 $n\geqslant 3$,所以这个数等于
$
\varphi(n)=\{x, 1 \leqslant x \leqslant n, \operatorname{gcd}(x, n)=1\}
$
为了证明这一点,考虑 $[0,n-1]$ 的一个第二型漂亮排列.沿顺时针方向在圆周上标记位置 $0,\ldots,n-1\pmod{n}$,使得数 $0$ 位于位置 $0$.记位置 $i$ 上的数为 $f(i)$;注意 $f$ 是 $[0,n-1]$ 的一个置换.设位置 $a$ 上的数是 $n-1$,即 $f(a)=n-1$.
因为除了 $0$ 以外所有的数都在一个 $n$ -弦中,且 $n$ -弦全体是顺次的,并且 $0$ 两侧的两个位置的连线是一条 $n$ -弦,所以所有的 $n$ -弦是平行的
(此时假设各点间距相同),即对于任意的 $i$,我们有
$f(i)+f(-i)=n$
类似地,因为 $(n-1)$ -弦全体是顺次的,且每个点都属于一条 $(n-1)$ -弦,
所以这些弦互相都是平行的,且对于任意的 $i$,有
$f(i)+f(a-i)=n-1$
所以对于任意的 $i$,$f(a-i)=f(-i)-1$;而由于 $f(0)=0$,我们得到对于任意的 $k$,
$f(-a k)=k$ ①
上面这个等式是模 $n$ 意义下的.因为 $f$ 是一个置换,我们必有 $(a,n)=1$,即
$
L_{n-1} \leqslant \varphi(n)
$
为证明等号成立.只需注意到 ① 给出的是一个漂亮排列.为此我们考虑圆周上满足 $w+y=x+z$ 的四个数 $w,x,y,z$.它们在圆周上的位置满足
$(-aw)+(-ay)=(-ax)+(-az)$.
即连结 $w$ 和 $y$ 的弦与连结 $x$ 和 $z$ 的弦是平行的.这样 ① 是漂亮的,且由构造可知这是第二型的.即得证明.
证法二
我们要注意到,题目的条件决定了圆周上的标记点的间距是无关紧要的,决定相关的弦是否相交的,仅仅是各点之间的次序关系.注意到 $(0,1)$ 中恰有 $N$ 个分母不超过 $n$ 的既约分数 $f_1 <\ldots< f_N$,因为每个满足 $x+y\leqslant n$,且 $\text{gcd}(x,y)=1$ 的正整数对 $(x,y)$ 都对应到分数 $\dfrac{x}{(x+y)}$.对于 $1\leqslant i\leqslant N$,记 $f_i = \dfrac{a_i}{b_i}$.
我们首先来构造 $N+1$ 个漂亮排列.考虑不等于上述 $N$ 个分数的任意一个 $\alpha\in(0,1)$.取一个周长为 $1$ 的圆周.我们顺次在圆上标记点 $0,1,2,\ldots,n$.其中 $0$ 点的位置是任意的,而从 $i$ 到 $i+1$ 我们沿顺时针方向前进 $\alpha$.这样标记 $k$ 的点到标记 $0$ 的点的顺时针方向的距离就是 $\{k\alpha\}$,其中 $\{r\}$ 表示 $r$ 的小数部分.称这样的一个漂亮排列是循环的,记为 $A(\alpha)$.如果 $A(\alpha_1)$ 和 $A(\alpha_2)$ 的各标记点的顺时针次序是相同的,
我们就认为它们是同一个标记方式.
 图是 $[1,13]$ 对于某个充分小的 $\varepsilon >0$ 的 $A(\dfrac{3}{5}+\varepsilon)$.
图是 $[1,13]$ 对于某个充分小的 $\varepsilon >0$ 的 $A(\dfrac{3}{5}+\varepsilon)$.如果 $a<b<c<d$ 满足 $a+d=b+c$,那么 $a\alpha+d\alpha=b\alpha+c\alpha$,所以在 $A(\alpha)$ 中连接标记 $a$ 和 $d$ 的点的弦与连结标记 $b$ 和 $c$ 的点的弦是平行的.这样在每个循环排列中,对于任意的 $k$,所有 $k$ -弦都是相互平行的.从而每一个循环排列都是漂亮的.
下面我们来说明恰好有 $N+1$ 种不同的循环排列.为此考察当 $\alpha$ 从 $0$ 递增到 $1$ 时 $A(\alpha)$ 的变化方式.标记 $p$ 的点和标记 $q$ 时点的位置顺序发生改变当且仅当 $\alpha$ 满足 $\{p\alpha\}=\{q\alpha\}$;而这种情况只会在 $\alpha$ 等于前述 $N$ 个分数之一的时候发生.这样最多就只能有 $N+1$ 种不同的循环排列.
要证明这些循环排列的确是两两不同的.对于充分小的 $\varepsilon>0$,和某个 $f_i=\frac{a_i}{b_i}$,考虑 $A(f_i +\varepsilon)$.那么标记为 $k$ 的点的(顺时针)位置在 $\frac{ka_{i}\pmod{b_i}}{b_i}+k\varepsilon$.这样所有的点可以根据这个位置表达式的第一项的值分成 $b_i$ 组.介于 $\frac{k}{b_i}$ 和 $\frac{k+1\pmod{b_i}}{b_i}$ 之间的点所标记的数对应的是 $ka_{i}^{-1}\pmod{b_i}$ 在 $0$ 到 $n$ 之间的不同取值(且按照从小到大依次排列).这样在 $A(f_i +\varepsilon)$ 中,
从 $0$ 出发,顺时针方向的第一个标记数是 $b_i$,而从 $0$ 出发往顺时针方向碰到的第一个比 $b_i$ 小的数是 $a_{i}^{-1}\pmod{b_i}$,而由这个数可以唯一地确定 $a_i$.这样从一个循环排列出发我们可以唯一地确定 $f_i$.同时注意到上述定义的循环排列 $A(f_i + \varepsilon)$ 是不包括顺时针方向顺次写上 $0,1,2,\ldots,n$ 这样一个"平凡"排列的,所以我们可以知道 $N+1$ 个循环排列 $A(\varepsilon),A(f_1 +\varepsilon),\ldots,A(f_N +\varepsilon)$ 是两两不同的.
下面我们观察到一个有用的事实:
如果 $f_i < \alpha < f_{i+1}$,那么在 $A(\alpha)$ 中从 $0$ 出发,顺时针方向第一个数是 $b_i$,逆时针方向第一个数是 $b_{i+1}$.②
事实上,我们已经对 $A(\alpha)=A(f_i +\varepsilon)$ 证明了前半部分,用同样的理由可以对 $A(\alpha)=A(f_{i+1}-\varepsilon)$ 证明后半部分.
最后,我们通过用对于 $n$ 的归纳来证明 $[0,n]$ 的所有漂亮标记都是循环排列.对于 $n=3$,这是显然的.现在假设 $[0,n-1]$ 的所有漂亮标记方法都是循环排列.我们考虑 $[0,n]$ 的一个漂亮标记方法 $A$.这样 $A_{n-1}=A\{n\}$ 是 $[0,n-1]$ 的一个漂亮标记方法,从而是一个循环排列.设 $A_{n-1}=A_{n-1}(\alpha)$.
假设在 $n-1$ 阶Farey序列(即分母不超过 $n-1$ 的 $(0,1)$ 之间的分数从小到大排列)中,$\alpha$ 介于相邻的两个分数 $\frac{p_1}{q_1}<\frac{p_2}{q_2}$ 之间,因为对于 $0<i\leqslant n-1$,
都成立 $\frac{i}{n}<\frac{i}{n-1}\leqslant\frac{i+1}{n}$,
所以在 $n$ 阶Farey序列中,至多有一个分母为 $n$ 的分数夹在这两个分数之间.
情形一:$\frac{p_1}{q_1}$ 和 $\frac{p_2}{q_2}$ 之间没有分母为 $n$ 的分数.
首先设在 $A_n (\alpha)$ 中,$n$ 介于 $x$ 和 $y$ 之间(顺时针方向依次为 $x,n,y$).由前述事实 ②,我们知道 $0$ 两边的数分别是 $q_1$ 和 $q_2$.
所以 $x,y\geqslant 1$.
由前述讨论可以知道,$x=n-b_i$ 关于某个 $k$ 满足 $x\equiv ka_{i}^{-1}\pmod{b_i}$,而 $y$ 则是 $y\equiv (k+1)a_{i}^{-1}\pmod{b_i}$ 在 $[1,n]$ 中的最小解.
同理,$x-1=(n-1)-b_i$ 关于某个 $k'$ 满足 $x-1\equiv k'a_{i}^{-1}\pmod{b_i}$,这样 $y-1\equiv (k'+1)a_{i}^{-1}\pmod{b_i}$,而且是 $[0,n]$ 满足上述同余方程的数中最小的一个.
所以在 $A_n (\alpha)$ 中,$x,y,x-1,n-1,y-1$ 顺时针方向顺次出现
(可能出现 $x=y-1$ 或者 $y=x-1$ 的情况).
现在我们注意到 $A$ 和 $A_n (\alpha)$ 相比最多只有 $n$ 的位置可能不同.
在 $A$ 中,因为连结 $x$ 和 $n-1$ 的弦与连结 $x-1$ 和 $n$ 的弦不相交,所以(沿顺时针方向)$n$ 就一定在 $x$ 和 $n-1$ 之间.同理(沿顺时针方向)$n$ 也一定在 $n-1$ 和 $y$ 之间.这样(沿顺时针方向)$n$ 就必定在 $x$ 和 $y$ 之间,从而 $A$ 就是一个循环排列.
情形二:$\frac{p_1}{q_1}$ 和 $\frac{p_2}{q_2}$ 之间恰有一个分母为 $n$ 的分数.
此时有两个循环排列 $A_n (\alpha_1)$ 和 $A_n (\alpha_2)$,去掉 $n$ 以后都得到 $A_{n-1}(\alpha)$,分别对应与 $\frac{p_1}{q_1}<\alpha_1<\frac{i}{n}$ 和 $\frac{i}{n}<\alpha_2<\frac{p_2}{q_2}$.
在 $A_{n-1}(\alpha)$ 中,由前述事实 ② 可知顺时针方向连续顺次出现 $q_2 , 0 , q_1$.同理,在 $A_n (\alpha_1)$ 中,顺时针方向连续顺次出现 $q_2 , n , 0 ,q_1$;在 $A_n (\alpha_2)$ 中,顺时针方向连续顺次出现 $q_2 , 0 , n , q_1$.
 令 $x=q_2 , y=q_1$ 和情形1同样讨论可知在 $A$ 中,$n$ 也必然位于 $x$ 和 $y$ 之间,这样 $A$ 要么等价于 $A_n (\alpha_1)$,要么等价于 $A_n (\alpha_2)$.
令 $x=q_2 , y=q_1$ 和情形1同样讨论可知在 $A$ 中,$n$ 也必然位于 $x$ 和 $y$ 之间,这样 $A$ 要么等价于 $A_n (\alpha_1)$,要么等价于 $A_n (\alpha_2)$.综上所述,每一个漂亮的标记法都是一个循环排列.由此命题得证.
答案
解析
备注