由 $6$ 个单位正方形构成如下图形以及它的旋转或翻转所得到的图形统称为钩形.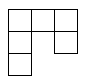 试确定所有 $m×n$ 的矩形,使其能被钩形所覆盖,要求:
试确定所有 $m×n$ 的矩形,使其能被钩形所覆盖,要求:
(1)覆盖矩形时,不能有空隙,钩形之间不重叠;
(2)钩形不能覆盖到矩形外.(爱沙尼亚)
 试确定所有 $m×n$ 的矩形,使其能被钩形所覆盖,要求:
试确定所有 $m×n$ 的矩形,使其能被钩形所覆盖,要求:(1)覆盖矩形时,不能有空隙,钩形之间不重叠;
(2)钩形不能覆盖到矩形外.(爱沙尼亚)
【难度】
【出处】
2004年第45届IMO试题
【标注】
【答案】
略
【解析】
证法一
所求的 $m,n$ 为满足 $3|m,4|n$ 或 $3|n,4|m$ 或 $12$ 整除 $m,n$ 之一而另一个不小于 $7$ 的正整数.
以下图形经过旋转或轴对称变换,视为等价.
如下图,给钩形的 $6$ 个格子编上号.图中阴影部分的格子必属于另一个钩形,且这个格子仅与该钩形中一个格子相邻,故只能是 $1$ 或 $6$ 这样的格子.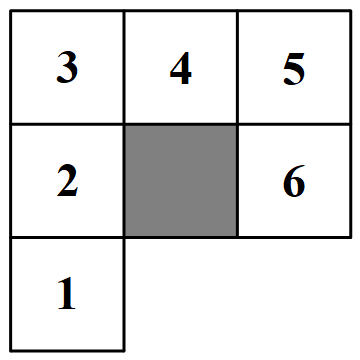
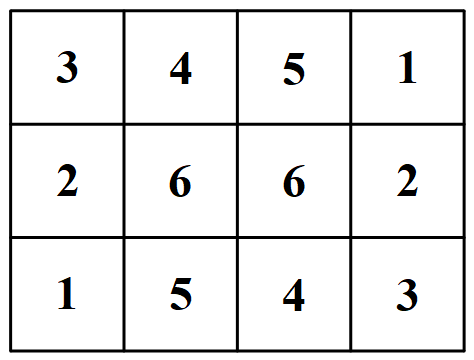 \[ ① \](i)如果是 $6$,则两个钩形形成一个 $3\times 4$ 的方块,称之为图形 ①.
\[ ① \](i)如果是 $6$,则两个钩形形成一个 $3\times 4$ 的方块,称之为图形 ①.
(ii)如果是 $1$,则有两种情形.
若为前者,则阴影部分的方格不被覆盖,矛盾.
因此只能是后者,称这个图形为 ②.
这样,图中的钩形就被两两配对,每对构成 ① 或 ②.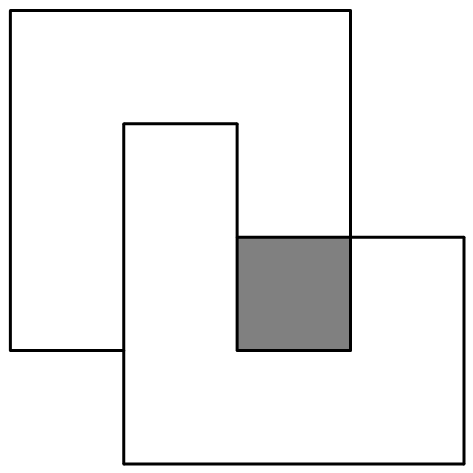
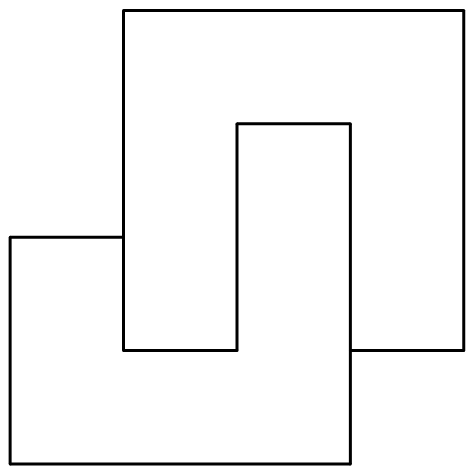 \[ ② \]由于 ①,② 均有 $12$ 个方格,故 $12|mn$.
\[ ② \]由于 ①,② 均有 $12$ 个方格,故 $12|mn$.
下面分三种情况:
(1)$3|m,4|n$ 或 $3|n,4|m$.
不妨设 $m=3m_0,n=4n_0$.将 ① 视为一个整体,用 $m_0n_0$ 个 ① 排成一个 $m_0\times n_0$ 的方阵即可,故这时 $m\times n$ 矩形能被钩形所覆盖(每个 $3\times 4$ 均可被两个钩形覆盖).
(2)$12|m$ 或 $12|n$,不妨设 $12|m$.
当 $3|n$ 或 $4|n$ 时,可化为(1).
当 $3\nmid n$ 且 $4\nmid n$ 时,由于图中至少有 $1$ 个 ① 或 ②,故 $n\geqslant 3$.从而 $n\geqslant 5$(因为 $3\nmid n,4\nmid n$).由于角上方格只能属于一个 ① 或 ②,而 $n\geqslant 5$ 说明相邻的两个角上的方格不能同属于一个 ① 或 ②,故 $n\geqslant 6$.又 $3\nmid n,4\nmid n$,故 $n\geqslant 7$.
下面说明 $n\geqslant 7( 3\nmid n,4\nmid n)$ 时一定能被钩形覆盖.
若 $n\equiv 1\pmod{3}$,则 $n=4+3t(t\in\mathbb{N}^{\ast})$.由(1)知 $12|m$ 时,$x\times 3t,m\times 4$ 均可被钩形覆盖.因此 $m\times n$ 可被钩形覆盖.
若 $n\equiv 2\pmod{3}$,则 $n=8+3t(t\in\mathbb{N}^{\ast})$.由(1)知 $12|m$ 时,$m\times 8,m\times 3t$ 均可被钩形覆盖.故 $m\times n$ 可被钩形覆盖.
(3)$12|mn$ 但 $4\nmid m,4\nmid n$.这时 $2|m,2|n$.不妨设 $m=6m_0,n=2n_0,2\nmid m_0,2\nmid n_0$.
下面证明这时 $m\times n$ 矩形不能被钩形覆盖.
考虑将 $m\times n$ 矩阵一列黑一列白地染色,则图中黑白格一样多,对于一个 ②,无论如何摆放,总盖住 $6$ 个黑格;对于一个横置的 ①,无论如何摆放,总盖住 $6$ 个黑格;而对于一个竖直的 ①,要么盖住 $8$ 个黑格,$4$ 个白格,要么盖住 $4$ 个黑格,$8$ 个白格.由于黑白格一样多,故盖住 $8$ 黑 $4$ 白和盖住 $4$ 黑 $8$ 白的一样多.从而竖直的 ① 有偶数个.同理可得(对行相间染色):横置的 ① 有偶数个.
考虑如下图将 $m\times n$ 矩形的格子分为 $4$ 类;$4$ 类的格子一样多,均为 $\dfrac{mn}{4}$ 个.
$\begin{array}{|c|c|c|c|c|c|c|c|c|}\hline
1&2&3&4&1&2&\cdots&1&2\\\hline
3&4&1&2&3&4&\cdots&3&4\\\hline
1&2&3&4&1&2&\cdots&1&2\\\hline
&&&&&&\cdots&&\\\hline
&&&&&&\cdots&&\\\hline
\vdots&\vdots&\vdots&\vdots&\vdots&\vdots&&\vdots&\vdots\\\hline
3&4&1&2&3&4&\cdots&3&4\\\hline
\end{array}$
对于一个 ①: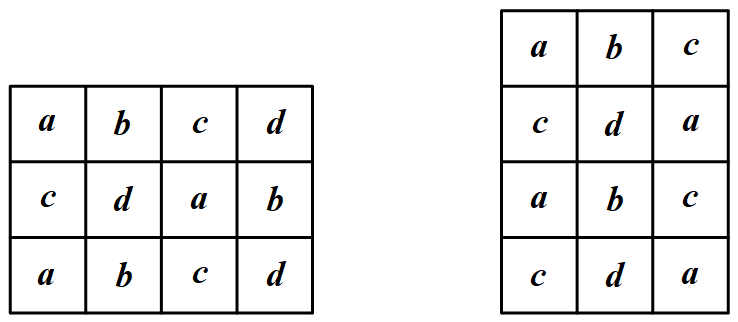 它盖住的 $a,c$ 一样多,$b,d$ 一样多,从而一个 ① 盖住的 $1,3$ 类格子一样多.
它盖住的 $a,c$ 一样多,$b,d$ 一样多,从而一个 ① 盖住的 $1,3$ 类格子一样多.
对于一个 ②: 由上图可以看出(i)(ii)两种盖住的 $1,3$ 类格子一样多,而(iii)(iv)两种 $1,3$ 类格子个数正好差 $2$,但 $m\times n$ 中 $1,3$ 类一样多.因此 $1$ 类比 $3$ 类多 $2$ 的和 $3$ 类比 $1$ 类多 $2$ 的一样多.从而(iii)(iv)两种的总数为偶数.若用
由上图可以看出(i)(ii)两种盖住的 $1,3$ 类格子一样多,而(iii)(iv)两种 $1,3$ 类格子个数正好差 $2$,但 $m\times n$ 中 $1,3$ 类一样多.因此 $1$ 类比 $3$ 类多 $2$ 的和 $3$ 类比 $1$ 类多 $2$ 的一样多.从而(iii)(iv)两种的总数为偶数.若用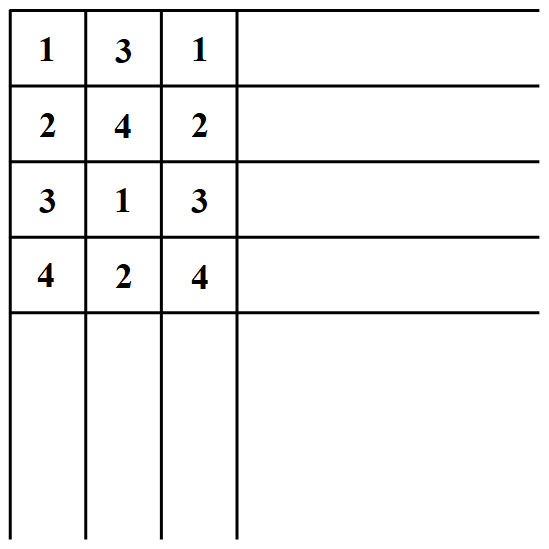 分类,类似可得(i)(ii)两种共有偶数个,从而 ② 有偶数个,所以共有偶数个 ① 和 ②.因而 $24|m\times n$,与 $4\nmid m,4\nmid n$ 矛盾.
分类,类似可得(i)(ii)两种共有偶数个,从而 ② 有偶数个,所以共有偶数个 ① 和 ②.因而 $24|m\times n$,与 $4\nmid m,4\nmid n$ 矛盾.
证法二
所有符合要求的数对 $m,n$ 是满足 $3|m,4|n$ 或 $3|n,4|m$ 或 $12|m,n\ne 1,2,5$ 或 $12|n,m\ne 1,2,5$ 的所有正整数对.
假设一个 $m\times n$ 的矩形能被钩形所覆盖.对任何钩形 $A$,存在唯一的钩形 $B$,使得它的"末端"的一个正方形覆盖 $A$ 的"内部"的一个正方形.同时,$B$ 的"内部"的正方形必须被 $A$ 的"末端"的一个正方形覆盖.这样,在 $m\times n$ 的一种覆盖中,所有的钩形两两配对,只有两种可能的方法放置 $B$,使得它与 $A$ 既不重叠也没有空隙.一种是 $A$ 和 $B$ 形成一个 $3\times 4$ 的矩形,另一种是形成一个八边形,边长依次为 $3,2,1,2,3,2,1,2$.
因此,一个 $m\times n$ 的矩形能被钩形覆盖当且仅当它能被加上两种 $12$ 个方形的块所覆盖.假定这样覆盖存在,则 $12|mn$,现在我们证明 $m,n$ 中至少有一个能被 $4$ 整除.
用反证法.假设 $m,n$ 均不能被 $4$ 整除,则由 $4|mn$ 知 $m,n$ 均为偶数.将 $m\times n$ 的矩形分成单位正方形,将行和列分别标上号码 $1,2,\cdots,m$ 及 $1,2,\cdots,n$.给单位正方形 $(i,j)$ 按如下方式赋值:值为 $i,j$ 小红能被 $4$ 整除的数的个数(因此值可以为 $0,1,2$).由于每一行和每一列的单位正方形的数目均为偶数,故所有赋值之和为偶数.每一个 $3\times 4$ 的矩形覆盖的数的和为 $3$ 或 $7$,另一种 $12$ 个方形的块覆盖的数的和为 $5$ 或 $7$.因此 $12$ 个正方形的块的总数是偶数,从而 $mn$ 能被 $24$ 整除,因而能被 $8$ 整除,与 $m,n$ 均不能被 $4$ 整除矛盾.
注意到 $m,n$ 均不能为 $1,2,5$.因此,若一个覆盖可能,则 $3$ 能整除 $m,n$ 之一,$4$ 能整除 $m,n$ 之一,且 $m,n\not\in\{1,2,5\}$.下面证明满足这些条件的 $m,n,m\times n$ 的矩形可被钩形所覆盖,事实上,只用 $3\times 4$ 的矩形即可.若 $3|m,4|n$ 或 $3|n,4|m$,则 $m\times n$ 可用 $3\times 4$ 的矩形覆盖.现设 $12|m,n\not\in\{1,2,5\}(12|n,m\not\in\{1,2,5\}$ 的情形一样),不妨设 $3\nmid n,4\nmid n$(否则归为前一情形).由于 $3\nmid n,4\nmid n$,故 $n\geqslant 7$ 且 $n-4,n-8$ 中至少有一个能被 $3$ 整除.因此 $m\times n$ 可被 $m\times 3,m\times 4$ 的矩形覆盖,从而能被 $3\times 4$ 的矩形覆盖.
所求的 $m,n$ 为满足 $3|m,4|n$ 或 $3|n,4|m$ 或 $12$ 整除 $m,n$ 之一而另一个不小于 $7$ 的正整数.
以下图形经过旋转或轴对称变换,视为等价.
如下图,给钩形的 $6$ 个格子编上号.图中阴影部分的格子必属于另一个钩形,且这个格子仅与该钩形中一个格子相邻,故只能是 $1$ 或 $6$ 这样的格子.

 \[ ① \](i)如果是 $6$,则两个钩形形成一个 $3\times 4$ 的方块,称之为图形 ①.
\[ ① \](i)如果是 $6$,则两个钩形形成一个 $3\times 4$ 的方块,称之为图形 ①.(ii)如果是 $1$,则有两种情形.
若为前者,则阴影部分的方格不被覆盖,矛盾.
因此只能是后者,称这个图形为 ②.
这样,图中的钩形就被两两配对,每对构成 ① 或 ②.

 \[ ② \]由于 ①,② 均有 $12$ 个方格,故 $12|mn$.
\[ ② \]由于 ①,② 均有 $12$ 个方格,故 $12|mn$.下面分三种情况:
(1)$3|m,4|n$ 或 $3|n,4|m$.
不妨设 $m=3m_0,n=4n_0$.将 ① 视为一个整体,用 $m_0n_0$ 个 ① 排成一个 $m_0\times n_0$ 的方阵即可,故这时 $m\times n$ 矩形能被钩形所覆盖(每个 $3\times 4$ 均可被两个钩形覆盖).
(2)$12|m$ 或 $12|n$,不妨设 $12|m$.
当 $3|n$ 或 $4|n$ 时,可化为(1).
当 $3\nmid n$ 且 $4\nmid n$ 时,由于图中至少有 $1$ 个 ① 或 ②,故 $n\geqslant 3$.从而 $n\geqslant 5$(因为 $3\nmid n,4\nmid n$).由于角上方格只能属于一个 ① 或 ②,而 $n\geqslant 5$ 说明相邻的两个角上的方格不能同属于一个 ① 或 ②,故 $n\geqslant 6$.又 $3\nmid n,4\nmid n$,故 $n\geqslant 7$.
下面说明 $n\geqslant 7( 3\nmid n,4\nmid n)$ 时一定能被钩形覆盖.
若 $n\equiv 1\pmod{3}$,则 $n=4+3t(t\in\mathbb{N}^{\ast})$.由(1)知 $12|m$ 时,$x\times 3t,m\times 4$ 均可被钩形覆盖.因此 $m\times n$ 可被钩形覆盖.
若 $n\equiv 2\pmod{3}$,则 $n=8+3t(t\in\mathbb{N}^{\ast})$.由(1)知 $12|m$ 时,$m\times 8,m\times 3t$ 均可被钩形覆盖.故 $m\times n$ 可被钩形覆盖.
(3)$12|mn$ 但 $4\nmid m,4\nmid n$.这时 $2|m,2|n$.不妨设 $m=6m_0,n=2n_0,2\nmid m_0,2\nmid n_0$.
下面证明这时 $m\times n$ 矩形不能被钩形覆盖.
考虑将 $m\times n$ 矩阵一列黑一列白地染色,则图中黑白格一样多,对于一个 ②,无论如何摆放,总盖住 $6$ 个黑格;对于一个横置的 ①,无论如何摆放,总盖住 $6$ 个黑格;而对于一个竖直的 ①,要么盖住 $8$ 个黑格,$4$ 个白格,要么盖住 $4$ 个黑格,$8$ 个白格.由于黑白格一样多,故盖住 $8$ 黑 $4$ 白和盖住 $4$ 黑 $8$ 白的一样多.从而竖直的 ① 有偶数个.同理可得(对行相间染色):横置的 ① 有偶数个.
考虑如下图将 $m\times n$ 矩形的格子分为 $4$ 类;$4$ 类的格子一样多,均为 $\dfrac{mn}{4}$ 个.
$\begin{array}{|c|c|c|c|c|c|c|c|c|}\hline
1&2&3&4&1&2&\cdots&1&2\\\hline
3&4&1&2&3&4&\cdots&3&4\\\hline
1&2&3&4&1&2&\cdots&1&2\\\hline
&&&&&&\cdots&&\\\hline
&&&&&&\cdots&&\\\hline
\vdots&\vdots&\vdots&\vdots&\vdots&\vdots&&\vdots&\vdots\\\hline
3&4&1&2&3&4&\cdots&3&4\\\hline
\end{array}$
对于一个 ①:
 它盖住的 $a,c$ 一样多,$b,d$ 一样多,从而一个 ① 盖住的 $1,3$ 类格子一样多.
它盖住的 $a,c$ 一样多,$b,d$ 一样多,从而一个 ① 盖住的 $1,3$ 类格子一样多.对于一个 ②:
 由上图可以看出(i)(ii)两种盖住的 $1,3$ 类格子一样多,而(iii)(iv)两种 $1,3$ 类格子个数正好差 $2$,但 $m\times n$ 中 $1,3$ 类一样多.因此 $1$ 类比 $3$ 类多 $2$ 的和 $3$ 类比 $1$ 类多 $2$ 的一样多.从而(iii)(iv)两种的总数为偶数.若用
由上图可以看出(i)(ii)两种盖住的 $1,3$ 类格子一样多,而(iii)(iv)两种 $1,3$ 类格子个数正好差 $2$,但 $m\times n$ 中 $1,3$ 类一样多.因此 $1$ 类比 $3$ 类多 $2$ 的和 $3$ 类比 $1$ 类多 $2$ 的一样多.从而(iii)(iv)两种的总数为偶数.若用 分类,类似可得(i)(ii)两种共有偶数个,从而 ② 有偶数个,所以共有偶数个 ① 和 ②.因而 $24|m\times n$,与 $4\nmid m,4\nmid n$ 矛盾.
分类,类似可得(i)(ii)两种共有偶数个,从而 ② 有偶数个,所以共有偶数个 ① 和 ②.因而 $24|m\times n$,与 $4\nmid m,4\nmid n$ 矛盾.证法二
所有符合要求的数对 $m,n$ 是满足 $3|m,4|n$ 或 $3|n,4|m$ 或 $12|m,n\ne 1,2,5$ 或 $12|n,m\ne 1,2,5$ 的所有正整数对.
假设一个 $m\times n$ 的矩形能被钩形所覆盖.对任何钩形 $A$,存在唯一的钩形 $B$,使得它的"末端"的一个正方形覆盖 $A$ 的"内部"的一个正方形.同时,$B$ 的"内部"的正方形必须被 $A$ 的"末端"的一个正方形覆盖.这样,在 $m\times n$ 的一种覆盖中,所有的钩形两两配对,只有两种可能的方法放置 $B$,使得它与 $A$ 既不重叠也没有空隙.一种是 $A$ 和 $B$ 形成一个 $3\times 4$ 的矩形,另一种是形成一个八边形,边长依次为 $3,2,1,2,3,2,1,2$.
因此,一个 $m\times n$ 的矩形能被钩形覆盖当且仅当它能被加上两种 $12$ 个方形的块所覆盖.假定这样覆盖存在,则 $12|mn$,现在我们证明 $m,n$ 中至少有一个能被 $4$ 整除.
用反证法.假设 $m,n$ 均不能被 $4$ 整除,则由 $4|mn$ 知 $m,n$ 均为偶数.将 $m\times n$ 的矩形分成单位正方形,将行和列分别标上号码 $1,2,\cdots,m$ 及 $1,2,\cdots,n$.给单位正方形 $(i,j)$ 按如下方式赋值:值为 $i,j$ 小红能被 $4$ 整除的数的个数(因此值可以为 $0,1,2$).由于每一行和每一列的单位正方形的数目均为偶数,故所有赋值之和为偶数.每一个 $3\times 4$ 的矩形覆盖的数的和为 $3$ 或 $7$,另一种 $12$ 个方形的块覆盖的数的和为 $5$ 或 $7$.因此 $12$ 个正方形的块的总数是偶数,从而 $mn$ 能被 $24$ 整除,因而能被 $8$ 整除,与 $m,n$ 均不能被 $4$ 整除矛盾.
注意到 $m,n$ 均不能为 $1,2,5$.因此,若一个覆盖可能,则 $3$ 能整除 $m,n$ 之一,$4$ 能整除 $m,n$ 之一,且 $m,n\not\in\{1,2,5\}$.下面证明满足这些条件的 $m,n,m\times n$ 的矩形可被钩形所覆盖,事实上,只用 $3\times 4$ 的矩形即可.若 $3|m,4|n$ 或 $3|n,4|m$,则 $m\times n$ 可用 $3\times 4$ 的矩形覆盖.现设 $12|m,n\not\in\{1,2,5\}(12|n,m\not\in\{1,2,5\}$ 的情形一样),不妨设 $3\nmid n,4\nmid n$(否则归为前一情形).由于 $3\nmid n,4\nmid n$,故 $n\geqslant 7$ 且 $n-4,n-8$ 中至少有一个能被 $3$ 整除.因此 $m\times n$ 可被 $m\times 3,m\times 4$ 的矩形覆盖,从而能被 $3\times 4$ 的矩形覆盖.
答案
解析
备注