设 $n\geqslant 2$ 为一个正整数，考虑由 ${{n}^{2}}$ 个单位正方格构成的 $n\times n$ 的正方形棋盘，一种放置 $n$ 个棋子“车”的方案被称为和平的，如果每一行每一列上正好有一个“车”。求最大的正整数 $k$ 使得对于任何一种和平放置 $n$ 个棋子“车”的方案，都存在一个 $k\times k$ 的棋盘使得它的 ${{k}^{2}}$ 个单位正方格中都没有“车”．（克罗地亚）
【难度】
【出处】
2014年第55届IMO试题
【标注】
【答案】
略
【解析】
答案：$[\sqrt{n-1}]$．
设 $l$ 是一个正整数，我们将证明以下两点，从而说明所求的最大值 $k_{\max}=[\sqrt{n-1}]$：
（1）如果 $n>l^2$，则对于任何一种和平放置 $n$ 个"车"的方案，都存在一个空的 $l\times l$ 正方形；
（2）如果 $n\leqslant l^2$，则存在一种和平放置 $n$ 个"车"的方案，使得每个 $l\times l$ 的正方形中都至少有一个"车"．
首先证明命题（1）．
当 $n>l^2$ 时，对于任何一种和平放置 $n$ 个"车"的方案，存在某一行 $R$ 使得这一行的第一个方格中有"车"．取 $l$ 个连续的行（包含行 $R$），它们的并集 $U$ 当中恰有 $l$ 个"车"．此时考察 $U$ 中的第 $2$ 列可第 $l^2 +1~(\leqslant n)$ 列，这个 $l\times l^2$ 的长方形可以划分为 $l$ 个 $l\times l$ 的正方形，但是其中最多有 $(l-1)$ 个"车"（因为 $U$ 中已有一个"车"在第 $1$ 列中），从而这 $l$ 个 $l\times l$ 的正方形中至少有一个是空的．
下面证明命题（2）．
为此我们将对于 $n=l^2$ 的情形先构造一个不含空的 $l\times l$ 正方形的和平放置方案．我们将所有的行依次标号 $0,1,2,\ldots ,l^2 -1$（从下到上），将所有的列也依次标号 $0, 1,2,\ldots, l^2 -1$（从左到右），并且将第 $r$ 行第 $c$ 列的单位正方形记为 $(r,c)$．
现在我们在所有形如 $(il+j,jl+i)$ 的单位正方形中各放一个"车"，其中 $i,j=0,1,2,\ldots,l-1$．如图显示了当 $l=3$ 时的放置方式．因为从 $0$ 到 $l^2 -1$ 中的每个数都有唯一的形如 $il+j$（$0\leqslant i, j\leqslant l-1$）的表示方法，所以每一行和每一列都恰好有一个"车"．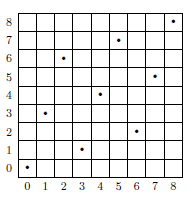
此时对于任意一个 $l\times l$ 正方形 $A$，设 $A$ 最下面一行的标号是 $pl+q$，其中 $0\leqslant p, q\leqslant l-1$（这是因为 $pl+q\leqslant l^2 - l$）．则 $A$ 所在的这 $l$ 行中有 $1$ 个"车"，
且这 $1$ 个"车"所在列的标号依次是 $ql+p,(q+1)l+p,\ldots,(l-1)l+p,p+1,l+(p+1),\ldots,(q-1)l+p+1$，将这些数从小到大排序为 $p+1,l+(p+1),\ldots,(q-1)l+p+1,ql+p,(q+1)l+p,\ldots,(l-1)l+p$．
这串数中相邻两个数的差不超过 $1$，第一个数不超过 $l-1$（如果 $p=l-1$，
则 $q=0$，那么第一个数将是 $ql+p=l-1$），最后一个数不小于 $(l-1)l$．
因此 $A$ 所在的列中全少有一个标号出现在这串数中，这也就意味着 $A$ 中包含至少一个"车"．这样对于 $n=l^2$ 的构造就完成了．
下面我们还需要对 $n<l^2$ 的情形构造不存在空的 $l\times l$ 正方形的和平放置方案．为此考察如上所述的 $l^{2}\times l^{2}$ 情形的构造，将其最右面的 $l^2 -n$ 列和最下面的 $l^2 -n$ 行删除，我们得到了一个 $n\times n$ 正方形，且其中不存在空的 $l\times l$ 正方形．但是其中一些行和列可能是空的，那么显然空行的数量与空列的数量是相等的，所以我们可以将这些行与列一一配对，然后在相对应的空行与空列的交叉处放入"车"，这样就得到了一个在 $n\times n$ 棋盘上和平放置 $n$ 个"车"的方案，并且其中不存在空的 $l \times l$ 正方形．
综合（1）和（2）的结论，所求的最大值 $k_{\max}=[\sqrt{n-1}]$．
设 $l$ 是一个正整数，我们将证明以下两点，从而说明所求的最大值 $k_{\max}=[\sqrt{n-1}]$：
（1）如果 $n>l^2$，则对于任何一种和平放置 $n$ 个"车"的方案，都存在一个空的 $l\times l$ 正方形；
（2）如果 $n\leqslant l^2$，则存在一种和平放置 $n$ 个"车"的方案，使得每个 $l\times l$ 的正方形中都至少有一个"车"．
首先证明命题（1）．
当 $n>l^2$ 时，对于任何一种和平放置 $n$ 个"车"的方案，存在某一行 $R$ 使得这一行的第一个方格中有"车"．取 $l$ 个连续的行（包含行 $R$），它们的并集 $U$ 当中恰有 $l$ 个"车"．此时考察 $U$ 中的第 $2$ 列可第 $l^2 +1~(\leqslant n)$ 列，这个 $l\times l^2$ 的长方形可以划分为 $l$ 个 $l\times l$ 的正方形，但是其中最多有 $(l-1)$ 个"车"（因为 $U$ 中已有一个"车"在第 $1$ 列中），从而这 $l$ 个 $l\times l$ 的正方形中至少有一个是空的．
下面证明命题（2）．
为此我们将对于 $n=l^2$ 的情形先构造一个不含空的 $l\times l$ 正方形的和平放置方案．我们将所有的行依次标号 $0,1,2,\ldots ,l^2 -1$（从下到上），将所有的列也依次标号 $0, 1,2,\ldots, l^2 -1$（从左到右），并且将第 $r$ 行第 $c$ 列的单位正方形记为 $(r,c)$．
现在我们在所有形如 $(il+j,jl+i)$ 的单位正方形中各放一个"车"，其中 $i,j=0,1,2,\ldots,l-1$．如图显示了当 $l=3$ 时的放置方式．因为从 $0$ 到 $l^2 -1$ 中的每个数都有唯一的形如 $il+j$（$0\leqslant i, j\leqslant l-1$）的表示方法，所以每一行和每一列都恰好有一个"车"．
此时对于任意一个 $l\times l$ 正方形 $A$，设 $A$ 最下面一行的标号是 $pl+q$，其中 $0\leqslant p, q\leqslant l-1$（这是因为 $pl+q\leqslant l^2 - l$）．则 $A$ 所在的这 $l$ 行中有 $1$ 个"车"，且这 $1$ 个"车"所在列的标号依次是 $ql+p,(q+1)l+p,\ldots,(l-1)l+p,p+1,l+(p+1),\ldots,(q-1)l+p+1$，将这些数从小到大排序为 $p+1,l+(p+1),\ldots,(q-1)l+p+1,ql+p,(q+1)l+p,\ldots,(l-1)l+p$．
这串数中相邻两个数的差不超过 $1$，第一个数不超过 $l-1$（如果 $p=l-1$，
则 $q=0$，那么第一个数将是 $ql+p=l-1$），最后一个数不小于 $(l-1)l$．
因此 $A$ 所在的列中全少有一个标号出现在这串数中，这也就意味着 $A$ 中包含至少一个"车"．这样对于 $n=l^2$ 的构造就完成了．
下面我们还需要对 $n<l^2$ 的情形构造不存在空的 $l\times l$ 正方形的和平放置方案．为此考察如上所述的 $l^{2}\times l^{2}$ 情形的构造，将其最右面的 $l^2 -n$ 列和最下面的 $l^2 -n$ 行删除，我们得到了一个 $n\times n$ 正方形，且其中不存在空的 $l\times l$ 正方形．但是其中一些行和列可能是空的，那么显然空行的数量与空列的数量是相等的，所以我们可以将这些行与列一一配对，然后在相对应的空行与空列的交叉处放入"车"，这样就得到了一个在 $n\times n$ 棋盘上和平放置 $n$ 个"车"的方案，并且其中不存在空的 $l \times l$ 正方形．
综合（1）和（2）的结论，所求的最大值 $k_{\max}=[\sqrt{n-1}]$．
答案
解析
备注
