重置
序号 ID 年级 类型 来源 摘要 创建时间
18036 5d2ffe99210b280220ed6407 高中 解答题 自招竞赛 巴斯银行发行的硬币在一面上铸有 $H$，在另一面上铸有 $T$．哈利有 $n$ 枚这样的硬币并将这些硬币从左至右排成一行．他反复地进行如下操作：如果恰有 $k(> 0)$ 枚硬币 $H$ 面朝上，则他将从左至右的第 $k$ 枚硬币翻转；如果所有硬币都是 $T$ 面朝上，则停止操作．例如：当 $n = 3$，并且初始状态是 $T HT$，则操作过程为 $T H T \rightarrow H H T \rightarrow H T T \rightarrow T T T$，总共进行了三次操作后停止．
（a）证明：对每个初始状态，哈利总在有限次操作后停止．
（b）对每个初始状态 $C$，记 $L(C)$ 为哈利从初始状态 $C$ 开始至停止操作时的操作次数，例如 $L(T H T)=3, L(T T T)=0$．求 $C$ 取遍所有 $2^n$ 个可能的初始状态时得到的 $L(C)$ 的平均值．（美国）		 2022-04-17 19:46:37
16226 5ffbd22c210b280319d00c7f 高中 解答题 高中习题 在一个足球联赛里有 $20$ 支足球队．第一轮他们分成 $10$ 对互相比赛，第二轮也分成 $10$ 对互相比赛．求证：在第三轮开赛前，可以找到 $10$ 支球队，他们两两没有赛过． 2022-04-17 19:53:20
16225 5ffbd2e5210b280319d00c86 高中 解答题 高中习题 平面上有 $10$ 个点，无三点共线，每两点之间用线段相连．每条线段都染上给定的 $k$ 种颜色之一，使得任意 $k$ 点之间的 $C_k^2$ 条线段都包含 $k$ 种颜色．求这样的整数 $k(1\leqslant 10\leqslant 10)$，
使得存在满足要求的染色方法．		 2022-04-17 19:52:20
16224 5ffbd380210b28031bc9259f 高中 解答题 高中习题 某地区网球俱乐部的 $20$ 名成员举行 $14$ 场单打比赛，每人至少上场一次．求证：必有 $6$ 场比赛，其中 $12$ 个参赛者各不相同． 2022-04-17 19:52:20
16223 5ffbddcb210b280319d00c8f 高中 解答题 高中习题 某次聚会共 $17$ 个人，其中每个人都恰好认识另外 $4$ 个人．证明：存在两人，他们彼此不认识且没有共同认识的人． 2022-04-17 19:51:20
16222 5ffbe44a210b280319d00c95 高中 解答题 高中习题 求最小的自然数 $n$，使得给人一个在 $10$ 个顶点，$n$ 条边的简单图的所用边进行红、蓝染色后，总存在单色三角形或单色四边形． 2022-04-17 19:51:20
16221 5ffbe4f7210b280319d00c9a 高中 解答题 高中习题 一个简单的 $n$ 阶图 $G$ 不含有三角形，则 $|E(G)|\leqslant [\frac{n^2}{4}]$． 2022-04-17 19:50:20
16220 5ffbea07210b280319d00ca2 高中 解答题 高中习题 记图 $G$ 中所有顶点的集合为 $V$，所有边的集合为 $E$．求证：若 $|E|\geqslant |V|+4$，则 $G$ 中必有两个无公共边的圈． 2022-04-17 19:49:20
16159 5ffbdb03210b28031bc925a8 高中 解答题 高中习题 证明：对任 $6$ 个人而言，要么存在 $3$ 个人两两认识，要么存在 $3$ 个人两两不认识；举例说明，如果改为 $5$ 个人的话，则结论不一定成立． 2022-04-17 19:16:20
15182 5ca41c6e210b281080bfd8b9 高中 解答题 自招竞赛 （1）证明：存在和为 $1$ 的五个非负实数 $a\text{,}b\text{,}c\text{,}d\text{,}e$，使得将它们任意放置在一个圆周上，总有两个相邻数的乘积不小于 $\frac{1}{9}$；（2）证明：对于和 $1$ 的任意五个非负实数 $a\text{,}b\text{,}c\text{,}d\text{,}e$，总可以将它们适当放置在一个圆周上，且任意相邻两数的乘积均不大于 $\frac{1}{9}$ 。 2022-04-17 19:23:11
15175 5ca423ec210b28107f52aa83 高中 解答题 自招竞赛 将一个 $3\times 3$ 的正方形的四个角上各去掉一个单位正方形所得到的图形称为“十字形”。在一个 $10\times 11$ 的棋盘上，最多可以放置多少个互不重叠的“十字形”（每个“十字形恰好盖住棋盘上的 $5$ 个小方格”）？ 2022-04-17 19:18:11
15172 5ca42835210b281080bfd92c 高中 解答题 自招竞赛 设正整数 $n\left( n\geqslant 3 \right)$ 。如果在平面上有 $n$ 个格点 ${{P}_{1}}\text{,}{{P}_{2}}\text{,}\cdots \text{,}{{P}_{n}}$ 满足：当 $\left| {{P}_{i}}{{P}_{j}} \right|$ 为有理数时，存在 ${{P}_{k}}$，使得 $\left| {{P}_{i}}{{P}_{k}} \right|$ 和 $\left| {{P}_{j}}{{P}_{k}} \right|$ 均为无理数；当 $\left| {{P}_{i}}{{P}_{j}} \right|$ 为无理数时，存在 ${{P}_{k}}$，使得 $\left| {{P}_{i}}{{P}_{k}} \right|$ 和 $\left| {{P}_{j}}{{P}_{k}} \right|$ 均为有理数，则称 $n$ 是“好数”。
（1）求最小的好数；（2）问：$2005$ 是否为好数？		 2022-04-17 19:16:11
15168 5ca56b05210b28107f52aaff 高中 解答题 自招竞赛 $8$ 个人参加一次聚会。（1）如果其中任何 $5$ 个人中都有 $3$ 个人两两认识，求证：可以从中找出 $4$ 个人两两认识；（2）试问：如果其中任何 $6$ 个人中都有 $3$ 个人两两认识，那么，是否一定可以找出 $4$ 个人两两认识？ 2022-04-17 19:13:11
15167 5ca56b0a210b28107f52ab04 高中 解答题 自招竞赛 平面上整点集 $S\text{=}\left\{ \left. \left( a\text{,}b \right) \right|1\leqslant a\text{,}b\leqslant 5\left( a\text{,}b\in Z \right) \right\}$，$T$ 为平面上一整点集，对 $S$ 中任一点 $P$，总存在 $T$ 中不同于 $P$ 的一点 $Q$，使得线段 $PQ$ 上除点 $P,Q$ 外无其他整点。问 $T$ 的元素个数最少为多少？ 2022-04-17 19:12:11
15166 5ca56b11210b281080bfd99b 高中 解答题 自招竞赛 设集合 $M\text{=}\left\{ 1\text{,}2\text{,}\cdots \text{,}19 \right\}\text{,}A\text{=}\left\{ {{a}_{1}}\text{,}{{a}_{2}}\text{,}\cdots \text{,}{{a}_{k}} \right\}\subseteq M$，求最小的 $k$，使得对任意的 $b\in M$，存在 ${{a}_{i}}\text{,}{{a}_{j}}\in A$，满足 $b\text{=}{{a}_{i}}$ 或 $b\text{=}{{a}_{i}}\pm {{a}_{j}}$（${{a}_{i}}\text{,}{{a}_{j}}$ 可以相同） 2022-04-17 19:12:11
15149 5caeda14210b280220ed1c6b 高中 解答题 自招竞赛 给定整数 $n\geqslant 2$．黑板上写着 $n$ 个集合，然后进行如下操作：选取黑板上两个互相不包含的集合 $A,B$，擦掉它们，然后写上 $A\bigcap B$ 和 $A\bigcup B$．这称为一次操作．如此操作下去，直到任意两个集合中都有一个包含另一个为止．对所有的初始状态和操作方式，求操作次数的最大可能值． 2022-04-17 19:03:11
15108 5d07293b210b280220ed468b 高中 解答题 自招竞赛 $MO$ 太空城由 $99$ 个空间站组成．任两空间站之间有管形通道相连．规定其中 $99$ 条通道为双向通行的主干道，其余通道严格单向通行．如果某四个空间站可以通过它们之间的通道从其中任一站到达另外任一站，则称这四个站的集合为一个互通四站组．
试为 $MO$ 太空城设计一个方案，使得互通四站组的数目最大（请具体算出该最大数，并证明你的结论）．		 2022-04-17 19:39:10
15102 5d103589210b280220ed4ac2 高中 解答题 自招竞赛 某公司需要录用一名秘书，共有 $ 10$ 人报名，公司经理决定按照求职报名的顺序逐个面试，前 $ 3$ 个人面试后一定不录 用．自第 $4$ 个人开始将他与前面面试过的人相比较，如果他的能力超过了前面所有已面试过的人，就录用他，否则就不录用，继续面试下一个．如果前 $9$ 个人都不录用，那么就录用最 后一个面试的人．
假定这 $10$ 个人的能力各不相同，可以按能力由强到弱排为第 $1$，第 $2$，…，第 $10$．显然该公司到底录用哪一个人，与这 $10$ 个人报名的顺序有关．大家知道，这样的排列共有 $10!$ 种 我们以 $A_k$ 表示能力第 $k$ 的人能够被录用的不同报名顺序的数目，以 $\dfrac{A_k}{10!}$ 表示他被录用的可能性．
证明：在该公司经理的方针之下，有
（1）$A_{1}>A_{2}>\cdots>A_{8}=A_{9}=A_{10}$；
（2）该公司有超过 $70\%$ 的可能性录取到能力最强的 $3$ 个人之一，而只有不超过 $10\%$ 的可能性录用到能力最弱的 $3$ 个人之一．		 2022-04-17 19:36:10
15099 5d105b1b210b280220ed4b6b 高中 解答题 自招竞赛 设 $M$ 是平面上 $n$ 个点组成的集合，满足：
（1）$M$ 中存在 $7$ 个点是一个凸七边形的 $7$ 个顶点；
（2）对 $M$ 中任意 $5$ 个点，若这 $5$ 个点是一个凸五边形的 $5$ 个顶点，则此凸五边形内部至少含有 $M $ 中的一个点．
求 $n$ 的最小值．		 2022-04-17 19:34:10
15095 5d1097da210b280220ed4c02 高中 解答题 自招竞赛 如图，圆形的水池被分割为 $2n(n\geqslant 5)$ 个“格子”．我们把有公共隔墙（公共边或公共弧）的“格子”称为相邻的，从而每个“格子”都有三个邻格．
水池中一共跳人了 $4n+ 1$ 只青蛙，青蛙难于安静共处，只 要某个“格子”中有不少于 $3$ 只青蛙，那么迟早一定会有其中 $3$ 只分别同时跳往三个不同邻格．证明：只要经过一段时间之后，青蛙便会在水池中大致分布均匀．
所谓大致分布均匀，就是任取其中一个“格子”，或者它里面有青蛙，或者它的三个邻格里都有青蛙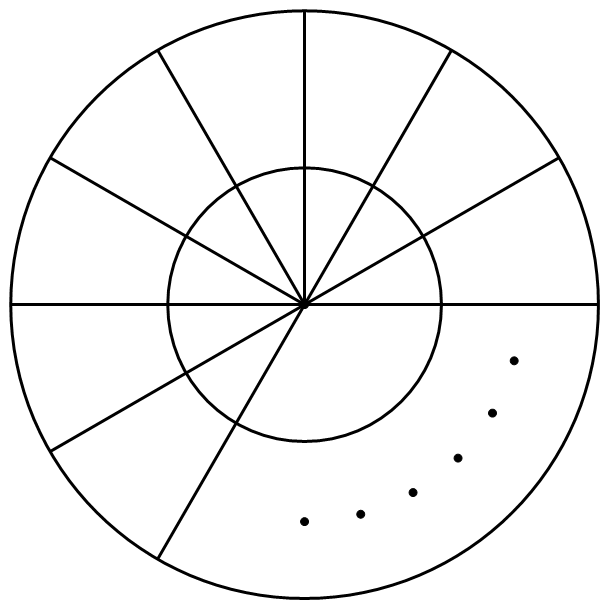．		 2022-04-17 19:33:10
0.184438s