设正整数 $n\left( n\geqslant 3 \right)$ 。如果在平面上有 $n$ 个格点 ${{P}_{1}}\text{,}{{P}_{2}}\text{,}\cdots \text{,}{{P}_{n}}$ 满足：当 $\left| {{P}_{i}}{{P}_{j}} \right|$ 为有理数时，存在 ${{P}_{k}}$，使得 $\left| {{P}_{i}}{{P}_{k}} \right|$ 和 $\left| {{P}_{j}}{{P}_{k}} \right|$ 均为无理数；当 $\left| {{P}_{i}}{{P}_{j}} \right|$ 为无理数时，存在 ${{P}_{k}}$，使得 $\left| {{P}_{i}}{{P}_{k}} \right|$ 和 $\left| {{P}_{j}}{{P}_{k}} \right|$ 均为有理数，则称 $n$ 是“好数”。
（1）求最小的好数；（2）问：$2005$ 是否为好数？
（1）求最小的好数；（2）问：$2005$ 是否为好数？
【难度】
【出处】
2005第4届CGMO试题
【标注】
【答案】
求最小的好数为 $5$，$2005$ 为好数
【解析】
我们断言最小的好数为 $5$，且 $2005$ 是好数。在三点组 $\left({{P}_{i}}\text{,}{{P}_{j}}\text{,}{{P}_{k}} \right)$ 中，$\left|{{P}_{i}}{{P}_{j}} \right|$ 为有理数（或无理数），$\left| {{P}_{i}}{{P}_{k}} \right|$、$\left|{{P}_{j}}{{P}_{k}} \right|$ 为无理数（或有理数），则称 $\left({{P}_{i}}\text{,}{{P}_{j}}\text{,}{{P}_{k}} \right)$ 为一个好组。
（1）$n\text{=}3$ 显然不是好数。 $n\text{=}4$ 也不是好数。若不然，假设 ${{P}_{1}}$、${{P}_{2}}$、${{P}_{3}}$、${{P}_{4}}$ 满足条件 。如图 $1$，不妨设 $\left| {{P}_{1}}{{P}_{2}} \right|$ 为有理数及 $\left({{P}_{1}}\text{,}{{P}_{2}}\text{,}{{P}_{3}} \right)$ 为一好组，则 $\left({{P}_{2}}\text{,}{{P}_{3}}\text{,}{{P}_{4}} \right)$ 为一好组。显然，$\left({{P}_{2}}\text{,}{{P}_{4}}\text{,}{{P}_{1}} \right)$ 和 $\left({{P}_{2}}\text{,}{{P}_{4}}\text{,}{{P}_{3}} \right)$ 均不是好组。所以，${{P}_{1}}$、${{P}_{2}}$、${{P}_{3}}$、${{P}_{4}}$ 不满足条件。矛盾。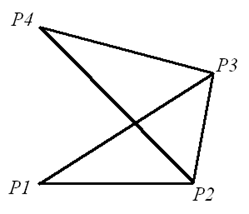
图1 $n\text{=}5$ 是好数。以下五个格点满足条件：${{A}_{5}}\text{=}\left\{ \left( 0\text{,}0 \right)\text{,}\left( 1\text{,}0\right)\text{,}\left( 5\text{,3} \right)\text{,}\left( 8\text{,}7\right)\text{,}\left( 0\text{,}7 \right) \right\}$ 。 
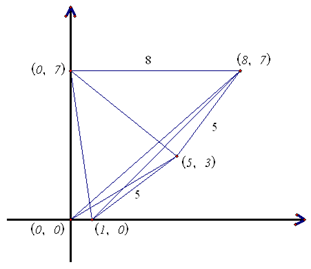图 $2$（2）设 $A\text{=}\left\{\left( 1\text{,}0 \right)\text{,}\left( 2\text{,}0 \right)\text{,}\cdots\text{,}\left( 669\text{,}0 \right) \right\}\text{,}B\text{=}\left\{ \left(1\text{,}1 \right)\text{,}\left( 2\text{,}1 \right)\text{,}\cdots\text{,}\left( 668\text{,}1 \right) \right\}\text{,}C\text{=}\left\{ \left(1\text{,}2 \right)\text{,}\left( 2\text{,}2 \right)\text{,}\cdots\text{,}\left( 668\text{,}2 \right) \right\}$ ${{S}_{2005}}\text{=}A\bigcup B\bigcup C$ 。对任意正整数 $n$，易证 ${{n}^{2}}+1$ 和 ${{n}^{2}}+4$ 不是完全平方数。不难证明，对于集合中任两点 ${{P}_{i}}$、${{P}_{j}}$，$\left| {{P}_{i}}{{P}_{j}} \right|$ 为有理数当且仅当 ${{P}_{i}}{{P}_{j}}$ 与某一坐标轴平行。所以 $2005$ 是好数。 注：当 $n\text{=}6$ 时，有 ${{A}_{6}}\text{=}{{A}_{5}}\bigcup\left\{ \left( -24\text{,}0 \right) \right\}$；当 $n\text{=}7$ 时，有 ${{A}_{7}}\text{=}{{A}_{6}}\bigcup\left\{ \left( -24\text{,}7 \right) \right\}$ 。可验证 $n\text{=}6\text{,}7$ 均为好数。当 $n\ge8$ 时，可像 $n\text{=}2005$ 那样排成三行，表明 $n\geqslant 8$ 时，所有的 $n$ 都是好数。
（1）$n\text{=}3$ 显然不是好数。 $n\text{=}4$ 也不是好数。若不然，假设 ${{P}_{1}}$、${{P}_{2}}$、${{P}_{3}}$、${{P}_{4}}$ 满足条件 。如图 $1$，不妨设 $\left| {{P}_{1}}{{P}_{2}} \right|$ 为有理数及 $\left({{P}_{1}}\text{,}{{P}_{2}}\text{,}{{P}_{3}} \right)$ 为一好组，则 $\left({{P}_{2}}\text{,}{{P}_{3}}\text{,}{{P}_{4}} \right)$ 为一好组。显然，$\left({{P}_{2}}\text{,}{{P}_{4}}\text{,}{{P}_{1}} \right)$ 和 $\left({{P}_{2}}\text{,}{{P}_{4}}\text{,}{{P}_{3}} \right)$ 均不是好组。所以，${{P}_{1}}$、${{P}_{2}}$、${{P}_{3}}$、${{P}_{4}}$ 不满足条件。矛盾。
图1 $n\text{=}5$ 是好数。以下五个格点满足条件：${{A}_{5}}\text{=}\left\{ \left( 0\text{,}0 \right)\text{,}\left( 1\text{,}0\right)\text{,}\left( 5\text{,3} \right)\text{,}\left( 8\text{,}7\right)\text{,}\left( 0\text{,}7 \right) \right\}$ 。 图 $2$（2）设 $A\text{=}\left\{\left( 1\text{,}0 \right)\text{,}\left( 2\text{,}0 \right)\text{,}\cdots\text{,}\left( 669\text{,}0 \right) \right\}\text{,}B\text{=}\left\{ \left(1\text{,}1 \right)\text{,}\left( 2\text{,}1 \right)\text{,}\cdots\text{,}\left( 668\text{,}1 \right) \right\}\text{,}C\text{=}\left\{ \left(1\text{,}2 \right)\text{,}\left( 2\text{,}2 \right)\text{,}\cdots\text{,}\left( 668\text{,}2 \right) \right\}$ ${{S}_{2005}}\text{=}A\bigcup B\bigcup C$ 。对任意正整数 $n$，易证 ${{n}^{2}}+1$ 和 ${{n}^{2}}+4$ 不是完全平方数。不难证明，对于集合中任两点 ${{P}_{i}}$、${{P}_{j}}$，$\left| {{P}_{i}}{{P}_{j}} \right|$ 为有理数当且仅当 ${{P}_{i}}{{P}_{j}}$ 与某一坐标轴平行。所以 $2005$ 是好数。 注：当 $n\text{=}6$ 时，有 ${{A}_{6}}\text{=}{{A}_{5}}\bigcup\left\{ \left( -24\text{,}0 \right) \right\}$；当 $n\text{=}7$ 时，有 ${{A}_{7}}\text{=}{{A}_{6}}\bigcup\left\{ \left( -24\text{,}7 \right) \right\}$ 。可验证 $n\text{=}6\text{,}7$ 均为好数。当 $n\ge8$ 时，可像 $n\text{=}2005$ 那样排成三行，表明 $n\geqslant 8$ 时，所有的 $n$ 都是好数。
答案
解析
备注
