将一个 $3\times 3$ 的正方形的四个角上各去掉一个单位正方形所得到的图形称为“十字形”。在一个 $10\times 11$ 的棋盘上，最多可以放置多少个互不重叠的“十字形”（每个“十字形恰好盖住棋盘上的 $5$ 个小方格”）？
【难度】
【出处】
2004第3届CGMO试题
【标注】
【答案】
$15$ 个
【解析】
首先证明最多可以放 $15$ 个“十字形”。 反证法。假设可放 $16$ 个“十字形”。对每个“十字形”，我们称其中心的方
格为“心”（记为*）。如图 $1$，将 $10\times11$ 的棋盘去掉周围一圈的方格，得到一个 $8\times 9$ 的方格表。显然每个“十字形”的“心”都只能出现在这个 $8\times9$ 的方格表中。（不可放置的格子用深色标记，下同）（图 $1$）
注意在每一个的 $3\times 3$ 方格表中最多可放两个“心”，如图 $2$ 所示。
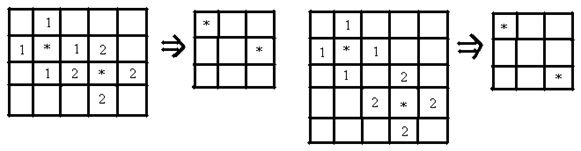（图 $2$）下面讨论，如何在一个 $8\times 3$ 的方格表中放入尽可能多的“心”。
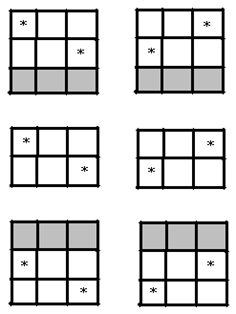（图 $3$）如图 $3$，将 $8\times 3$ 方格表自上至下分为 $3\times 3$，$2\times 3$，$3\times 3$ 的三个方格表。如果在中部 $2\times3$ 的方格表中至多放一个“心”，由于在每个 $3\times 3$ 的方格表中至多放 两个“心”，所以最终一共可以放入 $5$ 个“心”。如果在中部 $2\times 3$ 的方格表中放两个“心”，那么第三行和第六行都必须空着，通过枚举可知只能有 $3$ 的两种放置 $6$ 个“心”的方法。
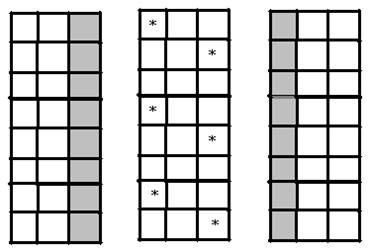（图 $4$）如图 $4$，我们将 $8\times 9$ 的方格表分为三个 $8\times 3$ 的方格表，自左至右依次称它们为 $\left( a\right)\text{,}\left( b \right)\text{,}\left( c \right)$ 。由于 $8\times 9$ 的方格表一共放入 $16$ 个“心”，所以必有一个 $8\times3$ 的方格表有 $6$ 个“心”。如果在 $\left( b \right)$ 中有 $6$ 个“心”，由于 $8\times3$ 的方格表中只有两种互相对称的放置 $6$ 个“心”的方法，故不妨设 $6$ 个“心”分布如图 $4$ 。易知此时第 $3$ 列和第 $7$ 列中不能放“心”。不难看出，在 $\left(a \right)$ 和 $\left( c \right)$ 中最多只能放 $4$ 个“心”。从而，一共放 $4+6+4\text{=}14$ 个“心”，矛盾。 如果在 $\left( a \right)\left( c \right)$ 各有 $6$ 个“心”，则第 $4$ 列和第 $6$ 列中都不能放“心”，从而 $\left(b \right)$ 中只有中间一列可以放“心”。不难看出，此时 $\left( b \right)$ 中最多只能放 $3$ 个“心”。从而，一共放 $6+3+6\text{=}15$ 个“心”，矛盾。如果 $\left(a \right)\left( c \right)$ 之一有 $6$ 个“心”，不妨设 $\left( a \right)$ 中有 $6$ 个“心”，且可设它们放置方式如图 $5$ 。此时第 $4$ 列中不能放“心”，从而 $\left(b \right)$ 中最多可以放 $4$ 个“心”，一共放 $6+4+5\text{=}15$ 个“心”，矛盾。
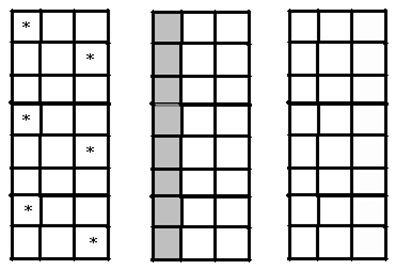（图5）综上所述，$8\times 9$ 的方格表中最多放置 $15$ 个“心”。 放置 $15$ 个“心”的两例构造如下：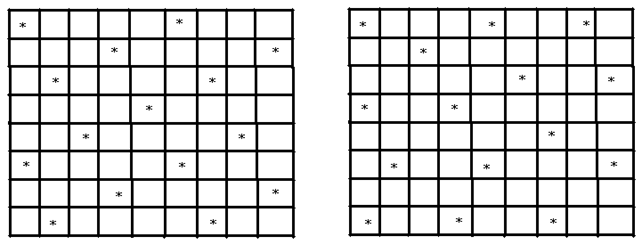
格为“心”（记为*）。如图 $1$，将 $10\times11$ 的棋盘去掉周围一圈的方格，得到一个 $8\times 9$ 的方格表。显然每个“十字形”的“心”都只能出现在这个 $8\times9$ 的方格表中。（不可放置的格子用深色标记，下同）（图 $1$）
注意在每一个的 $3\times 3$ 方格表中最多可放两个“心”，如图 $2$ 所示。（图 $2$）下面讨论，如何在一个 $8\times 3$ 的方格表中放入尽可能多的“心”。（图 $3$）如图 $3$，将 $8\times 3$ 方格表自上至下分为 $3\times 3$，$2\times 3$，$3\times 3$ 的三个方格表。如果在中部 $2\times3$ 的方格表中至多放一个“心”，由于在每个 $3\times 3$ 的方格表中至多放 两个“心”，所以最终一共可以放入 $5$ 个“心”。如果在中部 $2\times 3$ 的方格表中放两个“心”，那么第三行和第六行都必须空着，通过枚举可知只能有 $3$ 的两种放置 $6$ 个“心”的方法。（图 $4$）如图 $4$，我们将 $8\times 9$ 的方格表分为三个 $8\times 3$ 的方格表，自左至右依次称它们为 $\left( a\right)\text{,}\left( b \right)\text{,}\left( c \right)$ 。由于 $8\times 9$ 的方格表一共放入 $16$ 个“心”，所以必有一个 $8\times3$ 的方格表有 $6$ 个“心”。如果在 $\left( b \right)$ 中有 $6$ 个“心”，由于 $8\times3$ 的方格表中只有两种互相对称的放置 $6$ 个“心”的方法，故不妨设 $6$ 个“心”分布如图 $4$ 。易知此时第 $3$ 列和第 $7$ 列中不能放“心”。不难看出，在 $\left(a \right)$ 和 $\left( c \right)$ 中最多只能放 $4$ 个“心”。从而，一共放 $4+6+4\text{=}14$ 个“心”，矛盾。 如果在 $\left( a \right)\left( c \right)$ 各有 $6$ 个“心”，则第 $4$ 列和第 $6$ 列中都不能放“心”，从而 $\left(b \right)$ 中只有中间一列可以放“心”。不难看出，此时 $\left( b \right)$ 中最多只能放 $3$ 个“心”。从而，一共放 $6+3+6\text{=}15$ 个“心”，矛盾。如果 $\left(a \right)\left( c \right)$ 之一有 $6$ 个“心”，不妨设 $\left( a \right)$ 中有 $6$ 个“心”，且可设它们放置方式如图 $5$ 。此时第 $4$ 列中不能放“心”，从而 $\left(b \right)$ 中最多可以放 $4$ 个“心”，一共放 $6+4+5\text{=}15$ 个“心”，矛盾。（图5）综上所述，$8\times 9$ 的方格表中最多放置 $15$ 个“心”。 放置 $15$ 个“心”的两例构造如下：
答案
解析
备注
