（1）证明：存在和为 $1$ 的五个非负实数 $a\text{,}b\text{,}c\text{,}d\text{,}e$，使得将它们任意放置在一个圆周上，总有两个相邻数的乘积不小于 $\frac{1}{9}$；（2）证明：对于和 $1$ 的任意五个非负实数 $a\text{,}b\text{,}c\text{,}d\text{,}e$，总可以将它们适当放置在一个圆周上，且任意相邻两数的乘积均不大于 $\frac{1}{9}$ 。
【难度】
【出处】
2003第2届CGMO试题
【标注】
【答案】
略
【解析】
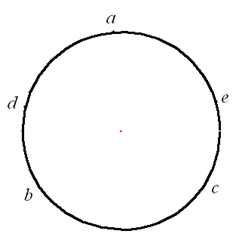（1）当 $a\text{=}b\text{=}c\text{=}\frac{1}{3}\text{,}d\text{=}e\text{=}0$ 时，把 $a\text{,}b\text{,}c\text{,}d\text{,}e$ 任意放置在一个圆周上，总有两个 $\frac{1}{3}$ 是相邻的，他们的乘积不小于 $\frac{1}{9}$ 。（2）不妨设 $a\geqslant b\geqslant c\geqslant d\geqslant e\geqslant 0$，把 $a\text{,}b\text{,}c\text{,}d\text{,}e$ 按图中所示放置。因为 $a+b+c+d+e\text{=}1$，所以 $a+3d\le1\text{,}a\cdot 3d\leqslant {{\left( \frac{a+3d}{2} \right)}^{2}}\leqslant \frac{1}{4}$ 。从而，$ad\leqslant \frac{1}{12}$ 。又因为 $a+b+c\leqslant 1$，所以 $b+c\leqslant \frac{2}{3}$ 。于是 $bc\leqslant\frac{{{\left( b+c \right)}^{2}}}{4}\leqslant \frac{1}{9}$ 。因为 $ce\leqslant ae\leqslant ad\text{,}bd\leqslant bc$，所以相邻两数的乘积均小于 $\frac{1}{9}$ 。
答案
解析
备注
