平面上整点集 $S\text{=}\left\{ \left. \left( a\text{,}b \right) \right|1\leqslant a\text{,}b\leqslant 5\left( a\text{,}b\in Z \right) \right\}$,$T$ 为平面上一整点集,对 $S$ 中任一点 $P$,总存在 $T$ 中不同于 $P$ 的一点 $Q$,使得线段 $PQ$ 上除点 $P,Q$ 外无其他整点。问 $T$ 的元素个数最少为多少?
【难度】
【出处】
2006第5届CGMO试题
【标注】
【答案】
最少个数为 $2$
【解析】
先证 $T$ 不可能只包含一个点。 若不然,设 $T\text{=}\left\{Q\left( {{x}_{0}}\text{,}{{y}_{0}} \right) \right\}$ 。在 $S$ 中取点 $P\left({{x}_{1}}\text{,}{{y}_{1}} \right)$ 满足 $\left( {{x}_{1}}\text{,}{{y}_{1}}\right)\ne \left( {{x}_{0}}\text{,}{{y}_{0}} \right)$,且 ${{x}_{1}}$ 与 ${{x}_{0}}$ 同奇偶,${{y}_{1}}$ 与 ${{y}_{0}}$ 同奇偶。则线段 $PQ$ 的中点为一整点,矛盾。 $T$ 包含两个点的情形如图。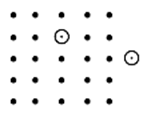

答案
解析
备注