设 $M$ 是平面上 $n$ 个点组成的集合，满足：
（1）$M$ 中存在 $7$ 个点是一个凸七边形的 $7$ 个顶点；
（2）对 $M$ 中任意 $5$ 个点，若这 $5$ 个点是一个凸五边形的 $5$ 个顶点，则此凸五边形内部至少含有 $M $ 中的一个点．
求 $n$ 的最小值．
（1）$M$ 中存在 $7$ 个点是一个凸七边形的 $7$ 个顶点；
（2）对 $M$ 中任意 $5$ 个点，若这 $5$ 个点是一个凸五边形的 $5$ 个顶点，则此凸五边形内部至少含有 $M $ 中的一个点．
求 $n$ 的最小值．
【难度】
【出处】
2004第19届CMO试题
【标注】
【答案】
略
【解析】
先证 $n\geqslant 11$．
设顶点在 $M$ 中的一个凸七边形为 $A_{1} A_{2} A_{3} A_{4} A_{5} A_{6} A_{7}$，联结 $A_1A_5$．由条件（1）知，在凸五边形 $A_{1} A_{2} A_{3} A_{4} A_{5}$ 中至少有 $M$ 中一个点，记为 $P_1$，联结 $P_{1} A_{1}, P_{1} A_{5}$，则在凸五边形 $A_{1} P_{1} A_{5} A_{6} A_{7}$ 内至少有 $M$ 中一个点，记为 $P_2$，且 $P_2$ 异于 $P_1$．联结直线 $P_1P_2$．则 $A_1,A_{2}, \cdots, A_{7}$ 中至少有 $5$ 个顶点不在直线 $P_1P_2$ 上，由抽屉原理知，在直线 $P_1P_2$ 的某一侧必有 $3$ 个顶点，这3个顶点与点 $P_1 , P_2$ 构成的凸五边形内，至少含有 $M$ 中的一 个点 $P_3$．
再作直线 $P_{1} P_{3}, P_{2} P_{3}$，令直线 $P_1P_2$ 对应区域 $\pi_3$；它是以直线 $P_1P_2$ 为边界且在 $\triangle P_1P_2P_3$ 异侧的一个半平面（不含直线 $P_1P_2$），类似地定义区域 $\pi_1,\pi_2$．这样，$3$ 个区域 $\pi_{1}, \pi_{2}, \pi_{3}$ 覆盖了平面上除 $\triangle P_1P_2P_3$ 外的所有点，由抽屉原理，$7$ 个顶点 $A_1,A_{2}, \cdots, A_{7}$ 中必有 $\left[\dfrac{7}{3}\right]+1=3$ 个顶点在同一区域（不妨设为 $\pi_3$）中，这 $3$ 点与 $P_1,P_2$ 构成一个顶点在 $M$ 中的凸五边形，故其内部至少含 $M$ 中一个点 $P_4$，所以 $n\geqslant 11$．
下面我们构造一个例子说明 $n = 11$ 是可以的．如图所示，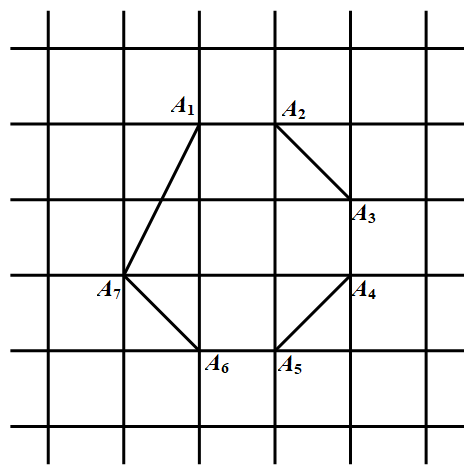
凸七边形 $A_{1} A_{2} A_{3} A_{4} A_{5} A_{6} A_{7}$ 为一整点七边形，其内部有 $4$ 个点，则条件（1）显然满足．这个点集 $M$ 也满足条件（2）．证明如下，用反证法，假设存在一个整点凸五边形，其内部不含整点．则因整点多边形的面积均可表示为 $\dfrac{n}{2}(n\in N_+)$ 的形式，由最小数原理，必有一个面积最小的内部不含整点的整点凸五边形 $ABCDE$．考虑顶点坐标的奇偶性，只有 $4$ 种情况：（奇，偶），（偶，奇），（奇，奇），（偶，偶）．从而五边形 $ABCDE$ 的顶点中必有两个顶点的坐标的奇偶性完全
相同，于是它们连线的中点 $P$ 仍为整点．又 $P$ 不在凸五边形 $ ABCDE$ 内部，从而 $P$ 在凸五边形的某条边上，不妨设 $P$ 在边 $AB$ 上，则 $P$ 为 $AB$ 的中点，联结 $PE$，则 $PBCDE$ 是面积更小的内部不含整点的整点凸五边形，矛盾．
综上所述，$n$ 的最小值为 $11$．
设顶点在 $M$ 中的一个凸七边形为 $A_{1} A_{2} A_{3} A_{4} A_{5} A_{6} A_{7}$，联结 $A_1A_5$．由条件（1）知，在凸五边形 $A_{1} A_{2} A_{3} A_{4} A_{5}$ 中至少有 $M$ 中一个点，记为 $P_1$，联结 $P_{1} A_{1}, P_{1} A_{5}$，则在凸五边形 $A_{1} P_{1} A_{5} A_{6} A_{7}$ 内至少有 $M$ 中一个点，记为 $P_2$，且 $P_2$ 异于 $P_1$．联结直线 $P_1P_2$．则 $A_1,A_{2}, \cdots, A_{7}$ 中至少有 $5$ 个顶点不在直线 $P_1P_2$ 上，由抽屉原理知，在直线 $P_1P_2$ 的某一侧必有 $3$ 个顶点，这3个顶点与点 $P_1 , P_2$ 构成的凸五边形内，至少含有 $M$ 中的一 个点 $P_3$．
再作直线 $P_{1} P_{3}, P_{2} P_{3}$，令直线 $P_1P_2$ 对应区域 $\pi_3$；它是以直线 $P_1P_2$ 为边界且在 $\triangle P_1P_2P_3$ 异侧的一个半平面（不含直线 $P_1P_2$），类似地定义区域 $\pi_1,\pi_2$．这样，$3$ 个区域 $\pi_{1}, \pi_{2}, \pi_{3}$ 覆盖了平面上除 $\triangle P_1P_2P_3$ 外的所有点，由抽屉原理，$7$ 个顶点 $A_1,A_{2}, \cdots, A_{7}$ 中必有 $\left[\dfrac{7}{3}\right]+1=3$ 个顶点在同一区域（不妨设为 $\pi_3$）中，这 $3$ 点与 $P_1,P_2$ 构成一个顶点在 $M$ 中的凸五边形，故其内部至少含 $M$ 中一个点 $P_4$，所以 $n\geqslant 11$．
下面我们构造一个例子说明 $n = 11$ 是可以的．如图所示，
凸七边形 $A_{1} A_{2} A_{3} A_{4} A_{5} A_{6} A_{7}$ 为一整点七边形，其内部有 $4$ 个点，则条件（1）显然满足．这个点集 $M$ 也满足条件（2）．证明如下，用反证法，假设存在一个整点凸五边形，其内部不含整点．则因整点多边形的面积均可表示为 $\dfrac{n}{2}(n\in N_+)$ 的形式，由最小数原理，必有一个面积最小的内部不含整点的整点凸五边形 $ABCDE$．考虑顶点坐标的奇偶性，只有 $4$ 种情况：（奇，偶），（偶，奇），（奇，奇），（偶，偶）．从而五边形 $ABCDE$ 的顶点中必有两个顶点的坐标的奇偶性完全相同，于是它们连线的中点 $P$ 仍为整点．又 $P$ 不在凸五边形 $ ABCDE$ 内部，从而 $P$ 在凸五边形的某条边上，不妨设 $P$ 在边 $AB$ 上，则 $P$ 为 $AB$ 的中点，联结 $PE$，则 $PBCDE$ 是面积更小的内部不含整点的整点凸五边形，矛盾．
综上所述，$n$ 的最小值为 $11$．
答案
解析
备注
