当 $0 < k < 1$ 时，关于 $x$ 的方程 $\left| {1 - {x^2}} \right| = kx + k$ 解的个数是 ．
【难度】
【出处】
无
【标注】
【答案】
$3$
【解析】
$x=-1$ 显然是方程的根．当 $x\neq -1$ 时，原方程等价于$$|x-1|\cdot\dfrac{|x+1|}{x+1}=k.$$考虑直线 $y=k$（$0<k<1$）和函数 $f(x)=|x-1|\cdot\dfrac{|x+1|}{x+1}$ 的图象公共点个数，如图．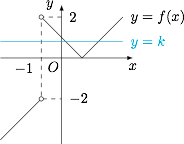
可得当 $x\neq -1$ 时，原方程有 $2$ 个解．综上所述，原方程的解的个数为 $3$．
可得当 $x\neq -1$ 时，原方程有 $2$ 个解．综上所述，原方程的解的个数为 $3$．
题目
答案
解析
备注
