查看数据源：59872e675ed01a0008fa5ef1
当 $0 < k < 1$ 时，关于 $x$ 的方程 $\left| {1 - {x^2}} \right| = kx + k$ 解的个数是 ．
【难度】
【出处】
无
【标注】
  • 知识点
    >
    函数
    >
    函数的图象与性质
    >
    函数的零点
  • 知识点
    >
    函数
    >
    常见初等函数
    >
    绝对值函数
  • 方法
    >
    代数处理
    >
    半分离变量法
【答案】
$3$
【解析】
考虑到直线 $y=kx+k$ 恒过定点 $(-1,0)$，如图，于是原方程的解的个数为 $3$．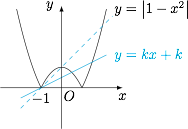
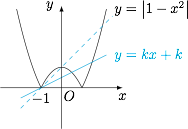
题目 答案 解析 备注
0.113291s