设函数 $ f\left(x\right)\left(x\in {\mathbb{R}}\right) $ 满足 $ f\left(-x\right)=f\left(x\right)$,$f\left(x\right)=f\left(2-x\right) $,且当 $ x\in \left[0,1\right] $ 时,$ f\left(x\right)=x^3 $.又函数 $ g\left(x\right)=|x\cos \left({\mathrm \pi }x\right)| $,则函数 $ h\left(x\right)=g\left(x\right)-f\left(x\right)$ 在 $\left[ -{\dfrac{1}{2}},{\dfrac{3}{2}} \right]$ 上的零点个数为 \((\qquad)\)
【难度】
【出处】
2012年高考辽宁卷(理)
【标注】
【答案】
B
【解析】
原题转化为函数 $ f\left(x\right) $ 与 $ g\left(x\right) $ 的图象在 $ \left[-{\dfrac{1}{2}},{\dfrac{3}{2}}\right] $ 上有几个交点的问题.
可知函数 $ f\left(x\right) $ 为偶函数,故 $ f\left(x\right)=f\left(2-x\right)=f\left(x-2\right) $,所以函数 $ f\left(x\right) $ 是周期为 $ 2 $ 的函数.结合当 $ x\in \left[0,1\right] $ 时,$ f\left(x\right)=x^3 $,可以画出函数 $ f\left(x\right) $ 在 $\left[ -{\dfrac{1}{2}},{\dfrac{3}{2}} \right]$ 上的图象.
当 $ x={\dfrac{3}{2}},{\dfrac{1}{2}},0 $ 时,$ g\left(x\right)=0 $,当 $ x=1 $ 时,$ g\left(x\right)=1 $,且 $ g\left(x\right) $ 是偶函数,函数值非负,由此可画出函数 $ y=g\left(x\right) $ 和函数 $ y=f\left(x\right) $ 的图象如图所示,由图可知两图象有 $ 6 $ 个交点.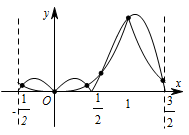
可知函数 $ f\left(x\right) $ 为偶函数,故 $ f\left(x\right)=f\left(2-x\right)=f\left(x-2\right) $,所以函数 $ f\left(x\right) $ 是周期为 $ 2 $ 的函数.结合当 $ x\in \left[0,1\right] $ 时,$ f\left(x\right)=x^3 $,可以画出函数 $ f\left(x\right) $ 在 $\left[ -{\dfrac{1}{2}},{\dfrac{3}{2}} \right]$ 上的图象.
当 $ x={\dfrac{3}{2}},{\dfrac{1}{2}},0 $ 时,$ g\left(x\right)=0 $,当 $ x=1 $ 时,$ g\left(x\right)=1 $,且 $ g\left(x\right) $ 是偶函数,函数值非负,由此可画出函数 $ y=g\left(x\right) $ 和函数 $ y=f\left(x\right) $ 的图象如图所示,由图可知两图象有 $ 6 $ 个交点.

题目
答案
解析
备注