$\triangle ABC$ 是边长为 $2$ 的等边三角形，已知向量 $\overrightarrow{a}$，$\overrightarrow{b}$ 满足 $\overrightarrow{AB}=2\overrightarrow a$，$\overrightarrow{AC}=2\overrightarrow a+\overrightarrow b$，则下列结论中正确的是 ．（写出所有正确结论的序号）
① $\overrightarrow a$ 为单位向量；
② $\overrightarrow b$ 为单位向量；
③ $\overrightarrow a\perp \overrightarrow b$；
④ $\overrightarrow b\parallel \overrightarrow{BC}$；
⑤ $\left(4\overrightarrow a+\overrightarrow b\right)\perp \overrightarrow{BC}$．
① $\overrightarrow a$ 为单位向量；
② $\overrightarrow b$ 为单位向量；
③ $\overrightarrow a\perp \overrightarrow b$；
④ $\overrightarrow b\parallel \overrightarrow{BC}$；
⑤ $\left(4\overrightarrow a+\overrightarrow b\right)\perp \overrightarrow{BC}$．
【难度】
【出处】
2015年高考安徽卷（文）
【标注】
【答案】
①④⑤
【解析】
根据题意可得 $\overrightarrow a=\dfrac 12\overrightarrow {AB}$，$\overrightarrow b=\overrightarrow {BC}$．如图，在边长为 $2$ 的菱形 $ABCD$ 中，$\angle ABC=60^\circ$，$M$ 为 $AB$ 中点，则有 $\overrightarrow a=\overrightarrow {AM}$，$\overrightarrow b=\overrightarrow {AD}$．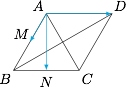
此时容易判断 ①④ 正确，而 ②③ 错误；
对于 ⑤，取线段 $BC$ 的中点 $N$，有 $2\overrightarrow a+\dfrac 12\overrightarrow b=\overrightarrow {AN}$，而 $\overrightarrow {AN}\perp \overrightarrow {BC}$，因此 $\left(4 \overrightarrow a+\overrightarrow b \right)\perp \overrightarrow {BC}$．
此时容易判断 ①④ 正确，而 ②③ 错误；对于 ⑤，取线段 $BC$ 的中点 $N$，有 $2\overrightarrow a+\dfrac 12\overrightarrow b=\overrightarrow {AN}$，而 $\overrightarrow {AN}\perp \overrightarrow {BC}$，因此 $\left(4 \overrightarrow a+\overrightarrow b \right)\perp \overrightarrow {BC}$．
题目
答案
解析
备注
