如图，$\angle AOB=30^\circ$，点 $M,N$ 分别是射线 $OA$，$OB$ 上的动点，$OP$ 平分 $\angle AOB$，且 $OP=6$，当 $\triangle PMN$ 的周长取最小值时，四边形 $PMON$ 的面积为 ．
【难度】
【出处】
无
【标注】
【答案】
$36\sqrt 3-54$
【解析】
分别作点 $P$ 关于 $OA,OB$ 的对称点 $C,D$，连接 $CD$，与 $OA,OB$ 的交点即为满足条件的点 $M,N$，连接 $OC,OD$，令 $CD$ 与 $OP$ 的交点为 $Q$．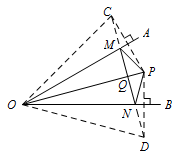
因为点 $P$ 关于 $OA,OB$ 的对称点 $C,D$，
所以 $ PM=CM$，$PN=DN$，$OC=OD=OP=6$，$\angle COA=\angle POA$，$\angle DOB=\angle POB$，
所以 $ \angle COD=60^\circ$，即 $\triangle COD$ 是等边三角形，
所以 $ CD=OC=OD=6$．
因为 $ OP$ 平分 $\angle AOB$，
所以 $ OP\perp CD$，$CQ=DQ=3$，
所以 $ OQ=6\times \dfrac{\sqrt 3}{2}=3\sqrt 3$，
所以 $ PQ=6-3\sqrt 3$．
设 $MQ=x$，则 $PM=CM=3-x$，
所以 $ \left(3-x\right)^2-x^2=\left(6-3\sqrt 3\right)^2$，解得 $x=6\sqrt 3-9$．
所以 $ MN=12\sqrt 3-18$，
所以 $ S_{四边形PMON}=S_{\triangle OMN}+S_{\triangle PMN}=\dfrac 12 \cdot MN\cdot OP=36\sqrt 3-54$．
因为点 $P$ 关于 $OA,OB$ 的对称点 $C,D$，所以 $ PM=CM$，$PN=DN$，$OC=OD=OP=6$，$\angle COA=\angle POA$，$\angle DOB=\angle POB$，
所以 $ \angle COD=60^\circ$，即 $\triangle COD$ 是等边三角形，
所以 $ CD=OC=OD=6$．
因为 $ OP$ 平分 $\angle AOB$，
所以 $ OP\perp CD$，$CQ=DQ=3$，
所以 $ OQ=6\times \dfrac{\sqrt 3}{2}=3\sqrt 3$，
所以 $ PQ=6-3\sqrt 3$．
设 $MQ=x$，则 $PM=CM=3-x$，
所以 $ \left(3-x\right)^2-x^2=\left(6-3\sqrt 3\right)^2$，解得 $x=6\sqrt 3-9$．
所以 $ MN=12\sqrt 3-18$，
所以 $ S_{四边形PMON}=S_{\triangle OMN}+S_{\triangle PMN}=\dfrac 12 \cdot MN\cdot OP=36\sqrt 3-54$．
题目
答案
解析
备注
