如图，四边形 $ ABCD $ 中，$\angle C={50^ \circ }$，$\angle B=\angle D={90^ \circ }$，$ E,F $ 分别是 $BC,DC$ 上的点，当 $\triangle AEF$ 的周长最小时，$\angle EAF$ 的度数为 ．
【难度】
【出处】
无
【标注】
【答案】
${80^ \circ }$
【解析】
分别作点 $A$ 关于 $BC,CD$ 的对称点 $H,G$，连接 $GH$ 交 $BC$ 于 $E$，交 $CD$ 于 $F$．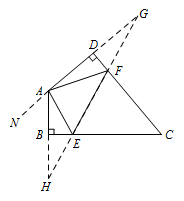
则 $GH$ 为 $\triangle AEF$ 的周长最小值，作 $DA$ 的延长线 $AN$．
因为 $ \angle C=50^\circ$，
所以 $\angle BAD=130^\circ$，
所以 $ \angle NAB=50^\circ$，
所以 $ \angle G+\angle H=50^\circ$．
因为 $\angle G=\angle DAF$，$\angle H=\angle BAE$，
所以 $ \angle DAF+\angle BAE=50^\circ$，
所以 $ \angle EAF=\angle BAD-\angle BAE-\angle DAF=130^\circ-50^\circ=80^\circ$．
则 $GH$ 为 $\triangle AEF$ 的周长最小值，作 $DA$ 的延长线 $AN$．因为 $ \angle C=50^\circ$，
所以 $\angle BAD=130^\circ$，
所以 $ \angle NAB=50^\circ$，
所以 $ \angle G+\angle H=50^\circ$．
因为 $\angle G=\angle DAF$，$\angle H=\angle BAE$，
所以 $ \angle DAF+\angle BAE=50^\circ$，
所以 $ \angle EAF=\angle BAD-\angle BAE-\angle DAF=130^\circ-50^\circ=80^\circ$．
题目
答案
解析
备注
