如图，已知正方形 $ABCD$ 边长为 $3$，点 $E$ 在 $AB$ 边上且 $BE=1$，点 $P,Q$ 分别是边 $BC,CD$ 的动点（均不与顶点重合）当四边形 $AEPQ$ 的周长取最小值时，四边形 $AEPQ$ 的面积是 ．
【难度】
【出处】
无
【标注】
【答案】
$\dfrac 92$
【解析】
如图，作正方形 $A'B'CD$ 和正方形 $A''B'CD'$，其中正方形 $A'B'CD$ 与正方形 $ABCD$ 关于 $CD$ 成轴对称，正方形 $A''B'CD'$ 与正方形 $ABCD$ 关于点 $C$ 成中心对称．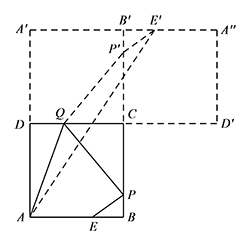
点 $P'$ 在 $CB'$ 上，满足 $CP'=CP$，点 $E'$ 在 $A''B'$ 上，满足 $B'E'=BE$．连接 $P'Q,P'E'$，则 $P'Q=PQ,P'E'=PE$．
如图，当 $A,Q,P',E'$ 四点共线时，四边形 $AEPQ$ 的周长取最小值．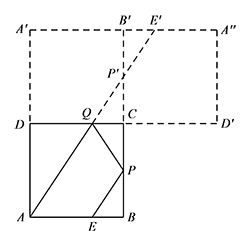
由 $\dfrac{DA}{DQ}=\dfrac{A'A}{A'E'}$，可得 $DQ=2$，
所以 $CQ=1$．
由 $\dfrac{CQ}{CP'}=\dfrac{B'E'}{B'P'}$，可得 $B'P'=CP'=\dfrac 32$，
所以 $BP=CP=\dfrac 32$．
所以 $S_{四边形AEPQ}=S_{正方形ABCD}-S_{\triangle ADQ}-S_{\triangle PCQ}-S_{\triangle PBE}=\dfrac 92$．
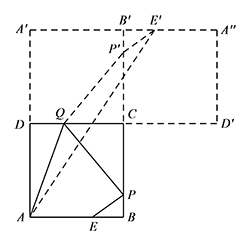点 $P'$ 在 $CB'$ 上，满足 $CP'=CP$，点 $E'$ 在 $A''B'$ 上，满足 $B'E'=BE$．连接 $P'Q,P'E'$，则 $P'Q=PQ,P'E'=PE$．如图，当 $A,Q,P',E'$ 四点共线时，四边形 $AEPQ$ 的周长取最小值．
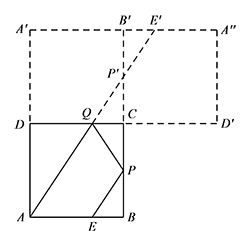由 $\dfrac{DA}{DQ}=\dfrac{A'A}{A'E'}$，可得 $DQ=2$，所以 $CQ=1$．
由 $\dfrac{CQ}{CP'}=\dfrac{B'E'}{B'P'}$，可得 $B'P'=CP'=\dfrac 32$，
所以 $BP=CP=\dfrac 32$．
所以 $S_{四边形AEPQ}=S_{正方形ABCD}-S_{\triangle ADQ}-S_{\triangle PCQ}-S_{\triangle PBE}=\dfrac 92$．
题目
答案
解析
备注
