如图，已知正方形 $ABCD$ 的边长为 $2$，$E$ 是边 $BC$ 上的动点，$BF\perp AE$ 交 $CD$ 于点 $F$，垂足为 $G$，连接 $CG$．下列说法：
① $AG>GE$；
② $AE=BF$；
③ 点 $G$ 运动的路径长为 ${\mathrm \pi}$；
④ $CG$ 的最小值为 $\sqrt 5-1$．
其中正确的说法是 ．（把你认为正确的说法的序号都填上）
① $AG>GE$；
② $AE=BF$；
③ 点 $G$ 运动的路径长为 ${\mathrm \pi}$；
④ $CG$ 的最小值为 $\sqrt 5-1$．
其中正确的说法是
【难度】
【出处】
无
【标注】
【答案】
②④
【解析】
因为 在正方形 $ABCD$ 中，$ BF\perp AE $，
所以 $ \angle AGB=90^\circ $ 不变，
所以 $ G$ 点的轨迹是以 $ AB $ 中点 $ O $ 为圆心，$ AO $ 为半径的圆弧．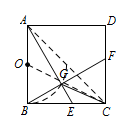
当 $E$ 移动到与 $C$ 重合时，$ F $ 点和 $ D $ 点重合，此时 $AG=GE$，故 ① 错误；
因为 $BF\perp AE$，
所以 $\angle AEB+\angle CBF=90^\circ $．
因为 $ \angle AEB+\angle BAE=90^\circ $，
所以 $ \angle BAE=\angle CBF$，
所以 $ \triangle ABE\cong \triangle BCF$（${\mathrm {AAS}}$），
所以 $AE=BF$．
故 ② 正确；
因为当 $ E $ 点运动到 $ C $ 点时停止，
所以 点 $ G $ 运动的轨迹是 $ \dfrac 14 $ 圆．
可得轨迹为 $ \dfrac {\mathrm \pi} {2} $，故 ③ 错误；
$CG$ 的最小值为 $OC-OG= \sqrt 5-1$，故 ④ 正确；
综上所述，正确的结论有 ②④．
所以 $ \angle AGB=90^\circ $ 不变，
所以 $ G$ 点的轨迹是以 $ AB $ 中点 $ O $ 为圆心，$ AO $ 为半径的圆弧．
当 $E$ 移动到与 $C$ 重合时，$ F $ 点和 $ D $ 点重合，此时 $AG=GE$，故 ① 错误；因为 $BF\perp AE$，
所以 $\angle AEB+\angle CBF=90^\circ $．
因为 $ \angle AEB+\angle BAE=90^\circ $，
所以 $ \angle BAE=\angle CBF$，
所以 $ \triangle ABE\cong \triangle BCF$（${\mathrm {AAS}}$），
所以 $AE=BF$．
故 ② 正确；
因为当 $ E $ 点运动到 $ C $ 点时停止，
所以 点 $ G $ 运动的轨迹是 $ \dfrac 14 $ 圆．
可得轨迹为 $ \dfrac {\mathrm \pi} {2} $，故 ③ 错误；
$CG$ 的最小值为 $OC-OG= \sqrt 5-1$，故 ④ 正确；
综上所述，正确的结论有 ②④．
题目
答案
解析
备注
