如图，已知 $\triangle ABC$ 的面积为 $1$，分别以 $AB,AC,BC$ 为边向外作正方形 $ABDE,ACFG,BCHI$，连接 $EG,FH,ID$．则以 $EG,FH,ID$ 的长度为三边长的三角形的面积等于 ．
【难度】
【出处】
无
【标注】
【答案】
$3$
【解析】
如图，分别过 $I,H$ 作 $AB,AC$ 的平行线，两线交于点 $M$，连接 $AM,EM,GM$．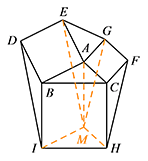
则 $\triangle EGM$ 是以 $EG,FH,ID$ 的长度为三边长的一个三角形．
由"等腰直角三角形共顶点模型"中的结论，
可得 $S_{\triangle BDI}=S_{\triangle CFH}=S_{\triangle EAG}=S_{\triangle ABC}$，
所以 $S_{\triangle EGM}=3S_{\triangle ABC}=3$．
则 $\triangle EGM$ 是以 $EG,FH,ID$ 的长度为三边长的一个三角形．由"等腰直角三角形共顶点模型"中的结论，
可得 $S_{\triangle BDI}=S_{\triangle CFH}=S_{\triangle EAG}=S_{\triangle ABC}$，
所以 $S_{\triangle EGM}=3S_{\triangle ABC}=3$．
题目
答案
解析
备注
