在如图的正方形方格纸中，每个小的四边形都是相同的正方形，$A,B,C,D$ 都在格点处，$AB$ 与 $CD$ 相交于点 $O$，则 $\tan \angle BOD$ 的值等于 ．
【难度】
【出处】
无
【标注】
【答案】
$3$
【解析】
如图，将 $CD$ 平移到 $C'D'$ 的位置，此时 $C'D'$ 与 $AB$ 交于格点 $P$．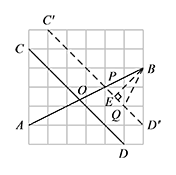
显然 $\angle BPD'=\angle BOD$．
在 $C'D'$ 上取格点 $Q$，使得 $BQ=BP=\sqrt 5$．
过点 $B$ 作 $BE\perp C'D'$ 于点 $E$，则 $PE=\dfrac 12PQ=\dfrac{\sqrt 2}2$，
从而 $BE=\sqrt{PB^2-PE^2}=\dfrac{3\sqrt 2}2$．
所以 $\tan \angle BOD=\tan \angle BPD'=\dfrac{BE}{PE}=3$．
显然 $\angle BPD'=\angle BOD$．在 $C'D'$ 上取格点 $Q$，使得 $BQ=BP=\sqrt 5$．
过点 $B$ 作 $BE\perp C'D'$ 于点 $E$，则 $PE=\dfrac 12PQ=\dfrac{\sqrt 2}2$，
从而 $BE=\sqrt{PB^2-PE^2}=\dfrac{3\sqrt 2}2$．
所以 $\tan \angle BOD=\tan \angle BPD'=\dfrac{BE}{PE}=3$．
题目
答案
解析
备注
