如图，在平面内，线段 $AB=6$，$P$ 为线段 $AB$ 上的动点，三角纸片 $CDE$ 的边 $CD$ 所在的直线与线段 $AB$ 垂直相交于点 $P$，且满足 $PC=PA$．若点 $A$ 沿 $AB$ 方向从点 $A$ 运动到点 $B$，则点 $E$ 运动的路径长为 ．
【难度】
【出处】
无
【标注】
【答案】
$6\sqrt 2$
【解析】
如图，连接 $AC$，显然 $\triangle PAC$ 为等腰直角三角形．
过点 $B$ 作 $BF\perp AB$，交 $AC$ 的延长线于点 $F$．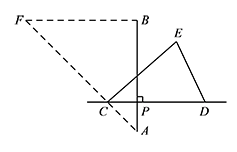
则 $AF$ 即为点 $C$ 的运动轨迹．
根据平移的性质可得，点 $E$ 的运动轨迹与点 $C$ 的运动轨迹平行且相等．
而 $AF=\sqrt 2AB=6\sqrt 2$，
所以点 $C$ 的运动轨迹长为 $6\sqrt 2$．
过点 $B$ 作 $BF\perp AB$，交 $AC$ 的延长线于点 $F$．
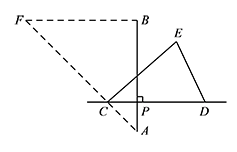则 $AF$ 即为点 $C$ 的运动轨迹．根据平移的性质可得，点 $E$ 的运动轨迹与点 $C$ 的运动轨迹平行且相等．
而 $AF=\sqrt 2AB=6\sqrt 2$，
所以点 $C$ 的运动轨迹长为 $6\sqrt 2$．
题目
答案
解析
备注
