已知复数 $z_1,z_2$ 满足 $|{z_1}| = 2$，$|{z_2}| = 3$，$|{z_1} + {z_2}| = 4$，则 $\dfrac{{{z_1}}}{{{z_2}}} = $ ．
【难度】
【出处】
2003年复旦大学保送生招生测试
【标注】
【答案】
$ \dfrac{1}{6} \pm \dfrac{{\sqrt {15} }}{6}{\rm{i}}$
【解析】
如图．设 $A,B$ 点对应的复数分别为 ${z_1}$，$ - {z_2}$，则 $\left| {OA} \right| = 2$，$\left| {OB} \right| = 3$，$\left| {AB} \right| = 4$．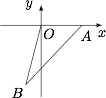
解 $\triangle OAB$，得$$\cos \angle AOB = \dfrac{{4 + 9 - 16}}{{2 \times 2 \times 3}} = - \dfrac{1}{4}.$$于是$$\dfrac{{{z_1}}}{{{z_2}}} = \dfrac{2}{3}\left( { \dfrac{1}{4} \pm \dfrac{{\sqrt {15} }}{4}{\rm{i}}} \right) = \dfrac{1}{6} \pm \dfrac{{\sqrt {15} }}{6}{\rm{i}}.$$
解 $\triangle OAB$，得$$\cos \angle AOB = \dfrac{{4 + 9 - 16}}{{2 \times 2 \times 3}} = - \dfrac{1}{4}.$$于是$$\dfrac{{{z_1}}}{{{z_2}}} = \dfrac{2}{3}\left( { \dfrac{1}{4} \pm \dfrac{{\sqrt {15} }}{4}{\rm{i}}} \right) = \dfrac{1}{6} \pm \dfrac{{\sqrt {15} }}{6}{\rm{i}}.$$
题目
答案
解析
备注
