双曲线 $C$ 的方程为 $x^2-\dfrac{y^2}{3}=1$，左、右焦点分别为 $F_1,F_2$，过点 $F_2$ 作一直线与双曲线 $C$ 的右半支交于点 $P,Q$，使得 $\angle F_1PQ=90^\circ$，则 $\triangle F_1PQ$ 的内切圆半径是 ．
【难度】
【出处】
2016年全国高中数学联赛（一试）
【标注】
【答案】
$\sqrt 7-1$
【解析】
如图，$F_1F_2=4$，$PF_1-PF_2=QF_1-QF_2=2$．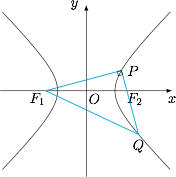
于是 $\triangle F_1PQ$ 的内切圆的半径\[\begin{split} r&=\dfrac 12\left(PF_1+PQ-F_1Q\right)\\
&=\dfrac 12\left(PF_1+PF_2+QF_2-F_1Q\right)\\
&=\dfrac 12\left[\sqrt{2\left(PF_1^{2}+PF_2^{2}\right)-\left(PF_1-PF_2\right)^2}-\left(QF_1-QF_2\right)\right]\\
&=\sqrt 7-1.\end{split}\]
于是 $\triangle F_1PQ$ 的内切圆的半径\[\begin{split} r&=\dfrac 12\left(PF_1+PQ-F_1Q\right)\\&=\dfrac 12\left(PF_1+PF_2+QF_2-F_1Q\right)\\
&=\dfrac 12\left[\sqrt{2\left(PF_1^{2}+PF_2^{2}\right)-\left(PF_1-PF_2\right)^2}-\left(QF_1-QF_2\right)\right]\\
&=\sqrt 7-1.\end{split}\]
题目
答案
解析
备注
