设函数 $f(x)=\dfrac 13x^3-3x^2+(8-a)x-5-a$，若存在唯一的正整数 $x_0$，使得 $f(x_0)<0$，则 $a$ 的取值范围是 ．
【难度】
【出处】
无
【标注】
【答案】
$\left(\dfrac{1}{15},\dfrac{1}{6}\right]$
【解析】
考虑到\[\begin{split} &f_1(a)=\dfrac 13-2a,\\ &f_2(a)=\dfrac 53-3a,\\ &f_3(a)=1-4a,\\ &f_4(a)=\dfrac 13-5a,\\ &f_5(a)=\dfrac 53-6a,\\ &f_6(a)=7-7a,\\ &\cdots \end{split}\]记 $f_n(a)=0$ 的零点为 $x_n$，则零点 $x_1,x_2,x_3,x_4,x_5$ 在数轴上分布如图，且容易证明 $x_n\geqslant 1$（$n\geqslant 6$）（因为 $a<\dfrac 16$，所以由 $f'(x)=x^2-6x+8-a$ 知，$f(x)$ 的极小值点 $3+\sqrt{a+1}<5$，所以不需要考虑 $n\geqslant 6$ 的情形）．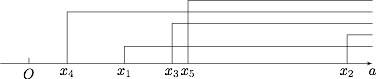
于是当 $x_4<a\leqslant x_1$ 时，$f(x)$ 存在唯一的正整数 $x_0=4$，使得 $f(x_0)<0$，此时 $a$ 的取值范围是 $\left(\dfrac{1}{15},\dfrac{1}{6}\right]$．
于是当 $x_4<a\leqslant x_1$ 时，$f(x)$ 存在唯一的正整数 $x_0=4$，使得 $f(x_0)<0$，此时 $a$ 的取值范围是 $\left(\dfrac{1}{15},\dfrac{1}{6}\right]$．
题目
答案
解析
备注
