在 $\triangle ABC$ 中，$B=120^\circ$，$AB=\sqrt 2$，$A$ 的角平分线 $AD=\sqrt 3$，则 $AC=$ ．
【难度】
【出处】
2015年高考重庆卷（理）
【标注】
【答案】
$\sqrt 6$
【解析】
根据已知示意图如下．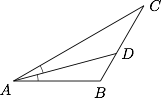
$\triangle ABD$ 中，应用正弦定理，得$$\dfrac{AD}{\sin B}=\dfrac{AB}{\sin \angle ADB},$$从而可得$$\sin\angle ADB=\dfrac{AB}{AD}\cdot\sin B=\dfrac{\sqrt 2}2,$$因此 $\angle ADB=45^\circ$，进而$$\angle ACB=\angle CAB=30^\circ,$$所以 $\triangle ABC$ 为等腰三角形，其底边 $AC$ 的长为$$2\cos 30^\circ \cdot AB=\sqrt 6.$$
$\triangle ABD$ 中，应用正弦定理，得$$\dfrac{AD}{\sin B}=\dfrac{AB}{\sin \angle ADB},$$从而可得$$\sin\angle ADB=\dfrac{AB}{AD}\cdot\sin B=\dfrac{\sqrt 2}2,$$因此 $\angle ADB=45^\circ$，进而$$\angle ACB=\angle CAB=30^\circ,$$所以 $\triangle ABC$ 为等腰三角形，其底边 $AC$ 的长为$$2\cos 30^\circ \cdot AB=\sqrt 6.$$
题目
答案
解析
备注
