查看数据源：591172a9e020e700094b099c
平面直角坐标系 $xOy$ 中，双曲线 $C_1:\dfrac{x^2}{a^2}-\dfrac{y^2}{b^2}=1\left(a>0,b>0\right)$ 的渐近线与抛物线 $C_2:x^2=2py\left(p>0\right)$ 交于 $O,A,B$．若 $\triangle OAB$ 的垂心为 $C_2$ 的焦点，则 $C_1$ 的离心率为 ．
【难度】
【出处】
2015年高考山东卷（理）
【标注】
  • 知识点
    >
    解析几何
    >
    双曲线
    >
    双曲线的几何量
    >
    双曲线的基本量
  • 知识点
    >
    解析几何
    >
    抛物线
    >
    抛物线的方程
    >
    抛物线的参数方程
【答案】
$\dfrac 32$
【解析】
设 $A(2pt,2pt^2)$，$B(-2pt,2pt^2)$，则 $\overrightarrow {AF}\cdot\overrightarrow {OB}=0$，即$$\left(-2pt,\dfrac p2-2pt^2\right)\cdot\left(-2pt,2pt^2\right)=0,$$解得 $t^2=\dfrac 54$．因此$$\dfrac{b^2}{a^2}=\left(\dfrac{2pt^2}{2pt}\right)^2=\dfrac 54,$$从而 $e=\dfrac 32$．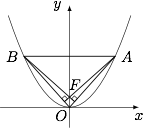
题目 答案 解析 备注
0.159501s