若直线 $y=kx+b$ 是曲线 $y=\ln x+2$ 的切线,也是曲线 $y=\ln (x+1)$ 的切线,则 $b=$ .
【难度】
【出处】
2016年高考全国甲卷(理)
【标注】
【答案】
$1-\ln 2$
【解析】
函数 $y=\ln x+2$ 的导函数为 $y'=\dfrac 1x$,函数 $y=\ln (x+1)$ 的导函数为 $y'=\dfrac{1}{x+1}$.设曲线 $y=\ln x+2$ 和曲线 $y=\ln (x+1)$ 上的切点横坐标分别为 $m,n$,则该直线方程可以写成$$y=\dfrac 1m\cdot (x-m)+\ln m+2,$$也可以写成$$y=\dfrac{1}{n+1}\cdot (x-n)+\ln (n+1),$$整理后对比得$$\begin{cases} \dfrac 1m=\dfrac{1}{n+1},\\ \ln m+1=\ln (n+1)-\dfrac{n}{n+1},\end{cases}$$解得$$\begin{cases} m=\dfrac 12,\\ n=-\dfrac 12,\end{cases}$$因此 $b=1-\ln 2$.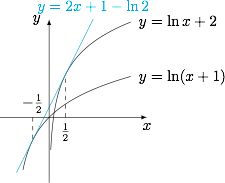
题目
答案
解析
备注