已知直线 $l:mx+y+3m-\sqrt 3=0$ 与圆 $x^2+y^2=12$ 交于 $A,B$ 两点，过 $A,B$ 分别作 $l$ 的垂线与 $x$ 轴交于 $C,D$ 两点，若 $|AB|=2\sqrt 3$，则 $|CD|=$ ．
【难度】
【出处】
2016年高考全国丙卷（理）
【标注】
【答案】
$4$
【解析】
由题意作图如下：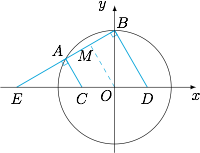
由 $|AB|=2\sqrt 3$ 知，圆心 $O$ 到直线 $l$ 的距离$$|OM|=\sqrt{12-\left(\dfrac 12|AB|\right)^2}=3,$$于是有$$\dfrac {\big|3m-\sqrt 3\big|}{\sqrt{m^2+1}}=3,$$解得$$m=-\dfrac {\sqrt 3}{3}.$$从而直线 $l$ 的倾斜角 $\angle BED=30^\circ$，
故$$|CD|=\dfrac {|AB|}{\cos 30^\circ}=4.$$
由 $|AB|=2\sqrt 3$ 知，圆心 $O$ 到直线 $l$ 的距离$$|OM|=\sqrt{12-\left(\dfrac 12|AB|\right)^2}=3,$$于是有$$\dfrac {\big|3m-\sqrt 3\big|}{\sqrt{m^2+1}}=3,$$解得$$m=-\dfrac {\sqrt 3}{3}.$$从而直线 $l$ 的倾斜角 $\angle BED=30^\circ$，故$$|CD|=\dfrac {|AB|}{\cos 30^\circ}=4.$$
题目
答案
解析
备注
