查看数据源：5922a70a623a97000c05dbfa
如图，$OA$ 在 $x$ 轴上，$OB$ 在 $y$ 轴上，$OA=8$，$AB=10$，点 $C$ 在边 $OA$ 上，$AC=2$，$\odot P$ 的圆心 $P$ 在线段 $BC$ 上，且 $\odot P$ 与边 $AB,AO$ 都相切．若反比例函数 $y= \dfrac kx\left(k\neq 0\right)$ 的图象经过圆心 $P$，则 $k=$  ．
【难度】
【出处】
无
【标注】
  • 题型
    >
    代几综合
    >
    函数与圆
【答案】
$-5$
【解析】
如图，过点 $P$ 作 $PD\perp OA$ 于点 $D$，作 $PE\perp AB$ 于点 $E$，过点 $C$ 作 $CH\perp AB$ 于点 $H$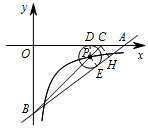．设 $\odot P$ 的半径为 $r$，
$\because \odot P$ 与边 $AB,AO$ 都相切，
$\therefore PD=PE=r$，$AD=AE$，
在 $\mathrm {Rt}\triangle OAB$ 中，$\because OA=8$，$AB=10$，
$\therefore OB=\sqrt{10^2-8^2} =6$，
$\because AC=2$，
$\therefore OC=6$，
$\therefore \triangle OBC$ 为等腰直角三角形，
$\therefore \triangle PCD$ 为等腰直角三角形，
$\therefore PD=CD=r$，
$\therefore AE=AD=2+r$，
$\because \angle CAH=\angle BAO$，
$\therefore \triangle ACH\backsim \triangle ABO$，
$\therefore \dfrac{CH}{OB} =\dfrac{AC}{AB} $，即 $ \dfrac{CH}{6}=\dfrac {2}{10} $，解得 $CH= \dfrac 65$，
$\therefore AH= \sqrt{AC^2-CH^2}=\sqrt{2^2-\left(\dfrac 65\right)^2} =\dfrac 85 $，
$\therefore BH=10-\dfrac 85 =\dfrac{42}{5} $，
$\because PE\parallel CH$，
$\therefore \triangle BEP\backsim \triangle BHC$，
$\therefore \dfrac{BE}{BH}= \dfrac{PE}{CH}$，即 $\dfrac{10-\left(2+r\right)}{\dfrac{42}{5}} =\dfrac{r}{\dfrac 65}$，解得 $r=1 $，
$\therefore OD=OC-CD=6-1=5$，
$\therefore P\left(5 ,-1\right)$，
$\therefore k=5\times\left(-1\right)=-5 $．
题目 答案 解析 备注
0.113668s