如图，$AD,BE$ 分别是 $\triangle ABC$ 的中线和角平分线，$AD\perp BE$，$AD=BE=6$，则 $AC$ 的长等于 ．
【难度】
【出处】
无
【标注】
【答案】
$\dfrac {9\sqrt 5}{2}$
【解析】
如图，延长 $AD$ 至点 $F$，使得 $DF=AD$，连接 $BF$，过点 $F$ 作 $FG\parallel BE$ 交 $AC$ 的延长线于点 $G$，过点 $C$ 作 $CH\parallel BE$ 交 $AF$ 于点 $H$．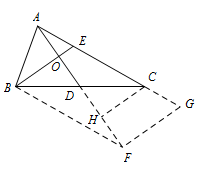
$\because$ $BE$ 是 $\triangle ABC$ 的角平分线，$AD\perp BE$，
$\therefore$ $AB=BD$，$AO=OD=3$．
易得 $\triangle ADC\cong \triangle FDB$，
$\therefore$ $ AC\parallel BF$，
又 $FG\parallel BE$，
$\therefore$ 四边形 $BEGF$ 为平行四边形．
$\therefore$ $BE=FG=6$，
$\because$ $AD=6$，
$\therefore$ $AF=12$．
在 ${\mathrm {Rt}}\triangle AFG$ 中，$AG=6\sqrt5$．
可证 $\triangle BOD\cong \triangle CHD$，
$\therefore$ $ DH=OD=3$，
$\therefore$ $ AH=9$，
$\therefore$ $ \dfrac{AH}{AF}=\dfrac{AC}{AG} $，
$\therefore$ $AC=\dfrac {9\sqrt 5}{2}$．
$\because$ $BE$ 是 $\triangle ABC$ 的角平分线，$AD\perp BE$，$\therefore$ $AB=BD$，$AO=OD=3$．
易得 $\triangle ADC\cong \triangle FDB$，
$\therefore$ $ AC\parallel BF$，
又 $FG\parallel BE$，
$\therefore$ 四边形 $BEGF$ 为平行四边形．
$\therefore$ $BE=FG=6$，
$\because$ $AD=6$，
$\therefore$ $AF=12$．
在 ${\mathrm {Rt}}\triangle AFG$ 中，$AG=6\sqrt5$．
可证 $\triangle BOD\cong \triangle CHD$，
$\therefore$ $ DH=OD=3$，
$\therefore$ $ AH=9$，
$\therefore$ $ \dfrac{AH}{AF}=\dfrac{AC}{AG} $，
$\therefore$ $AC=\dfrac {9\sqrt 5}{2}$．
题目
答案
解析
备注
