对于各数互不相等的整数数组 $(i_1,i_2,\cdots,i_n)$（$n$ 是不小于 $3$ 的正整数），若对任意的 $p,q\in\{1,2,\cdots,n\}$，当 $p<q$ 时有 $i_p>i_q$，则称 $i_p,i_q$ 是该数组的一个“逆序”．一个数组中所有“逆序”的个数称为该数组的“逆序数”，如数组 $(2,3,1)$ 的逆序数等于 $2$．则数组 $(5,2,4,3,1)$ 的逆序数等于 ；若数组 $(i_1,i_2,\cdots,i_n)$ 的逆序数为 $n$，则数组 $(i_n,i_{n-1},\cdots,i_1)$ 的逆序数为 ．
【难度】
【出处】
无
【标注】
【答案】
$(1)$ $8$；$(2)$ $\dfrac{n^2}{2}-\dfrac{3n}{2}$
【解析】
如图，将数组 $(5,2,4,3,1)$ 对应的散点图画出，数出其中斜率为负的线段条数即可．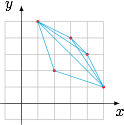
考虑到数组 $(i_1,i_2,\cdots,i_n)$ 与数组 $(i_n,i_{n-1},\cdots,i_1)$ 对应的散点图关于 $y=x$ 对称，因此数组 $(i_n,i_{n-1},\cdots,i_1)$ 中的逆序数为 $\mathrm{C}_n^2-n=\dfrac{n^2}{2}-\dfrac{3n}{2}$．
考虑到数组 $(i_1,i_2,\cdots,i_n)$ 与数组 $(i_n,i_{n-1},\cdots,i_1)$ 对应的散点图关于 $y=x$ 对称，因此数组 $(i_n,i_{n-1},\cdots,i_1)$ 中的逆序数为 $\mathrm{C}_n^2-n=\dfrac{n^2}{2}-\dfrac{3n}{2}$．
题目
答案
解析
备注
